题目内容
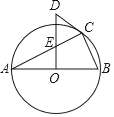
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D落在AB边上,斜边DE交AC于点F,则n的大小和图中阴影部分的面积分别为( )

A. 30,2 B. 60,2 C. 60,![]() D. 60,
D. 60,![]()
【答案】C
【解析】
先根据已知条件求出AC的长及∠B的度数,再根据图形旋转的性质及等边三角形的判定定理判断出△BCD的形状,进而得出∠DCF的度数,由直角三角形的性质可判断出DF是△ABC的中位线,由三角形的面积公式即可得出结论.
解答:解:∵△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,
∴∠B=60°,AC=BC×cot∠A=2×![]() =2
=2![]() ,AB=2BC=4,
,AB=2BC=4,
∵△EDC是△ABC旋转而成,
∴BC=CD=BD=![]() AB=2,
AB=2,
∵∠B=60°,
∴△BCD是等边三角形,
∴∠BCD=60°,
∴∠DCF=30°,∠DFC=90°,即DE⊥AC,
∴DE∥BC,
∵BD=![]() AB=2,
AB=2,
∴DF是△ABC的中位线,
∴DF=![]() BC=
BC=![]() ×2=1,CF=
×2=1,CF=![]() AC=
AC=![]() ×2
×2![]() =
=![]() ,
,
∴S阴影=![]() DF×CF=
DF×CF=![]() ×
×![]() =
=![]() .
.
故选C.

练习册系列答案
相关题目
【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
![]() 他们在一次实验中共掷骰子
他们在一次实验中共掷骰子![]() 次,试验的结果如下:
次,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最大.”她的说法正确吗?为什么?
点朝上的概率最大.”她的说法正确吗?为什么?
![]() 小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.