题目内容
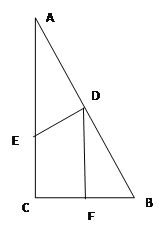
【题目】如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．
（1）若四边形AEDF的周长为24，AB=15，求AC的长；
（2）求证：EF垂直平分AD．
【答案】（1）AC=9；（2）见解析
【解析】试题分析:(1)因为在直角三角形中斜边上的中线等于斜边的一半,因此可证得:DE=AE=BE= 
,DF=AF=CF=
再根据四边形AEDF的周长和AB的边长可计算出AC,(2)由(1)可得:DE=AE,DF=AF,利用线段垂直平分线的判定定理可得,点E,F在线段AD的垂直平分线上,因此EF垂直平分AD.
试题解析:(1)因为AD⊥BC,
所以△ADB和△ADC是直角三角形,
因为点E是AB的中点,点F是AC的中点,
所以DE=AE= 
, DF=AF =
因为四边形形AEDF的周长是24,AB=15,
所以AC=24-15=9.
(2)因为DE=AE, DF=AF ,
所以点E在线段AD的垂直平分线上,点F在线段AD的垂直平分线上,
所以EF垂直平分AD.
练习册系列答案
走进文言文系列答案
相关题目
【题目】体育课上全班男生进行了百米测试，达标成绩为14秒，下面是第一小组8名男生的成绩记录，其中“+”表示成绩大于14秒，“﹣”表示成绩小于14秒
﹣1 | +0.8 | 0 | ﹣1.2 | ﹣0.1 | 0 | +0.5 | ﹣0.6 |
（1）求这个小组的男生达标率是多少？
（2）求这个小组8名男生的平均成绩是多少？
