题目内容
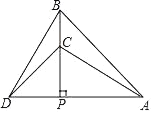
【题目】如图，△PAB与△PCD均为等腰直角三角形，点C在PB上，若△ABC与△BCD的面积之和为10，则△PAB与△PCD的面积之差为（ ）
A. 5B. 10C. l5D. 20
【答案】B
【解析】
由题意得，S△ABC+S△BCD＝
BCPA+BCPD＝BC(PA+PD)＝10，要求△PAB与△PCD的面积之差，即PA2﹣PB2＝ (PA+PD)(PA﹣PD)＝ (PB﹣PC)(PA+PD)＝BC(PA+PD)，即可求解.
解：依题意，
∵△PAB与△PCD均为等腰直角三角形
∴PB＝PB，PC＝PD
∴S△PAB﹣S△PCD＝PA2﹣PD2
＝(PA+PD)(PA﹣PD)
＝(PB﹣PC)(PA+PD)
＝BC(PA+PD)，
又∵S△ABC+S△BCD＝BCPA+BCPD＝BC(PA+PD)＝10
∴S△PAB﹣S△PCD＝10．
故选：B．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
【题目】“每天锻炼一小时，健康生活一辈子”．为了选拔“阳光大课间”领操员，学校组织初中三个年级推选出来的15名领操员进行比赛，成绩如下表：
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
（1）这组数据的众数是多少，中位数是多少．
（2）已知获得2018年四川省南充市的选手中，七、八、九年级分别有1人、2人、1人，学校准备从中随机抽取两人领操，求恰好抽到八年级两名领操员的概率．
