题目内容
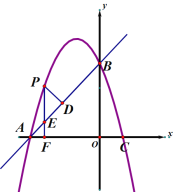
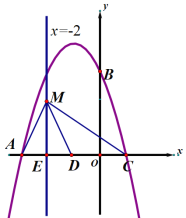
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,3),C(1,0).
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
(3)在直线![]() 上是否存在点M,使得∠MAC=2∠MCA,若存在,求出M点坐标.若不存在,说明理由.
上是否存在点M,使得∠MAC=2∠MCA,若存在,求出M点坐标.若不存在,说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)将A(3,0),B(0,3),C(1,0)三点的坐标代入y=ax2+bx+c,运用待定系数法即可求出此抛物线的解析式;
(2)先证明△AOB是等腰直角三角形,得出∠BAO=45°,再证明△PDE是等腰直角三角形,则PE越大,△PDE的周长越大,求出直线AB的解析式为y=x+3,设与AB平行的直线解析式为y=x+m,联立![]() ,
,![]() 时,PD最大,求出m即可得到P点坐标;
时,PD最大,求出m即可得到P点坐标;
(3)设直线![]() 与x轴交于点E,作点A关于直线
与x轴交于点E,作点A关于直线![]() 的对称点D,则D(-1,0),连接MA,MD,MC,由∠MAC =2∠MCA可得MD=CD=2,勾股定理求出ME=
的对称点D,则D(-1,0),连接MA,MD,MC,由∠MAC =2∠MCA可得MD=CD=2,勾股定理求出ME=![]() ,即可得M点坐标
,即可得M点坐标
解:(1)∵抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),C(1,0),
∴![]() ,
,
解得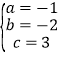 ,
,
所以,抛物线的解析式为![]() ;
;
(2)∵A(﹣3,0),B(0,3),
∴OA=OB=3,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=90°﹣45°=45°,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PD越大,△PDE的周长越大,
易得直线AB的解析式为y=x+3,
设与AB平行的直线解析式为y=x+m,
联立![]() ,
,
消掉y得,![]() ,
,
当![]() ,
,
即![]() 时,直线与抛物线只有一个交点,PD最长,
时,直线与抛物线只有一个交点,PD最长,
此时![]() ,
,
∴点![]() ,△PDE的周长最大;
,△PDE的周长最大;
(3)设直线![]() 与x轴交于点E,作点A关于直线
与x轴交于点E,作点A关于直线![]()
的对称点D,则D(-1,0),连接MA,MD,MC.
∴MA=MD,∠MAC=∠MDA=2∠MCA
∴∠CMD=∠DCM
∴MD=CD=2
∴ME=![]()
∴![]()

 阅读快车系列答案
阅读快车系列答案【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?