题目内容
如图所示,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.
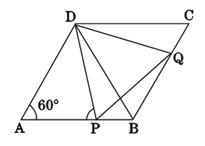
(1)求证:△BDQ≌△ADP;
(2)已知AD=3,AP=2,求cos∠BPQ的值 (结果保留根号)

(1)求证:△BDQ≌△ADP;
(2)已知AD=3,AP=2,求cos∠BPQ的值 (结果保留根号)
(1)证明可得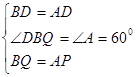 ∴△BDQ≌△ADP(SAS)(2)
∴△BDQ≌△ADP(SAS)(2)
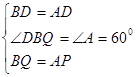 ∴△BDQ≌△ADP(SAS)(2)
∴△BDQ≌△ADP(SAS)(2)
试题分析:(1)证明:∵四边形ABCD是菱形,∵∠A=60°,

∴△ABD是等边三角形,∴BD=AD,∠ABD=60°
∵AD∥BC,∴∠DBQ=60°
在△BDQ与△ADP中,
∵
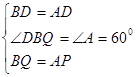 ∴△BDQ≌△ADP(SAS)
∴△BDQ≌△ADP(SAS) (2)解:∵△BDQ≌△ADP,∴∠BDQ=∠ADP,DQ=DP,∴∠PDQ=∠ADB=60°.
∴△DPQ是等边三角形.∴∠DPQ=60°
∵∠DPQ+∠BPQ=∠A+∠ADP,∴∠BPQ=∠ADP
过点P作PM⊥AD于M,在Rt△APM中,PM=AP.sin∠A=2sin600=
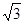 ,
,AM=AP.cos600=1,∴DM="3-1=2," 在Rt△PDM中,PD=
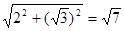
cos∠ADP=
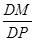 =
=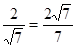 , ∴cos∠BPQ =cos∠ADP
, ∴cos∠BPQ =cos∠ADP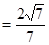
点评:本题考查全等三角形,三角函数,解答本题要求考生掌握三角形全等的判定方法,会证明两个三角形全等,熟悉三角函数的定义

练习册系列答案
相关题目

 ABC中,
ABC中,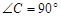 ,D为边CA延长线上一点,DE//AB,
,D为边CA延长线上一点,DE//AB, ADE=42
ADE=42 ,则
,则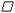 ABCD中,对角线AC与BD交于点O,∠BAD的平分线交直线BC于点E,交直线DC于点F.
ABCD中,对角线AC与BD交于点O,∠BAD的平分线交直线BC于点E,交直线DC于点F.

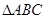 中,
中,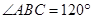 ,点
,点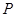 是底边
是底边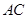 上一个动点,
上一个动点, 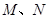 分别是
分别是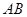 、
、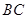 的中点.若
的中点.若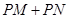 的最小值是2,则
的最小值是2,则