题目内容
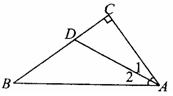
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.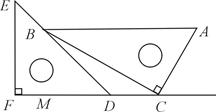

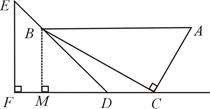
试题分析:过点B作BM⊥FD于点M.根据含30°角的直角三角形的性质可求得AB的长,在直角三角形BAC中根据勾股定理可求得BC的长,从而可求得MB的长,在直角三角形BMC中根据勾股定理可求得CM的长,再根据等腰直角三角形的性质求得MD的长,从而可以求得结果.
过点B作BM⊥FD于点M.
在△ACB中,∠ACB=90°,∠A=60°,AC=10
∴∠ABC=30°
∴AB=20,
在直角三角形BAC中,由勾股定理得BC=10
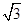
∵AB∥CF
∴∠BCM=30°
∴MB=5
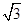
在直角三角形BMC中,由勾股定理得CM=15
在△EFD中,∠F=90°,∠E=45°
∴∠EDF=45°
∴
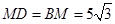
∴
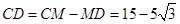 .
.点评:解直角三角形的应用是中考必考题,一般难度不大,正确作出辅助线构造直角三角形是解题关键.

练习册系列答案
相关题目