Question

【题目】如图，在平面直角坐标系中，抛物线y=﹣x2+2x+3与x轴的交点为A，B（点A在点B的左侧），与y轴的交点为C，连结BC．点M是抛物线上A，C之间的一个动点，过点M作MN∥BC，分别交x轴、抛物线于D，N，过点M作EF⊥x轴，垂足为F，并交直线BC于点E，

（1）求点A，B，C的坐标．
（2）当点M恰好是EF的中点，求BD的长．
（3）连接DE，记△DEM，△BDE的面积分别为S1 ， S2 ， 当BD=1时，则S2﹣S1= ．

Answer 1

【答案】
（1）

解：在y=﹣x2+2x+3中，令y=0可得﹣x2+2x+3=0，解得x=﹣1或x=3，

∴A（﹣1，0），B（3，0），

令x=0可得y=3，

∴C（0，3）；

（2）

解：∵B（3，0），C（0，3），

∴直线BC解析式为y=﹣x+3，

∵点M是抛物线上A，C之间的一个动点，

∴可设M（t，﹣t2+2t+3）（﹣1＜t＜0），则E（t，﹣t+3），

∴EF=﹣t+3，MF=﹣t2+2t+3，

∵M为EF的中点，

∴﹣t+3=2（﹣t2+2t+3），解得t=﹣ 或t=3（不符合题意，舍去），

∴F（﹣ ，0），

∴BF=3﹣（﹣ ）= ，

∵MN∥BC，

∴D为BF的中点，

∴BD= BF= ；

（3）
【解析】解：（3）如图，过D作DH∥EF，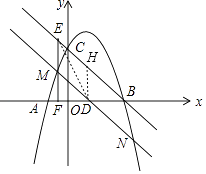

∵MN∥BC，
∴四边形DHEM为平行四边形，
∴S△DEM=S△DEH ，
∵DH⊥BD，且∠OBC=45°，
∴DH=BD=1，
∴S2﹣S1=S△HDB= BDDH= ×1×1= ，
所以答案是： ．