题目内容
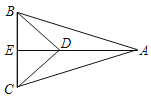
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)猜想:AD和CE是否垂直?若垂直,请说明理由.

【答案】(1)证明见解析;(2)垂直,理由见解析.
【解析】
(1)证明△ABD≌△CBE即可得出AD=CE;
(2)延长AD分别交BC和CE于G和F,由于△ABD≌△CBE,所以∠BAD=∠BCE从而可知∠AFC=∠ABC=90°,所以AD⊥CE.
解:(1)∵△ABC和△DBE均为等腰直角三角形
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=∠CBE,
在△ABD与△CBE中,
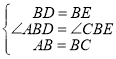 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE.
(2)垂直.延长AD分别交BC和CE于G和F,
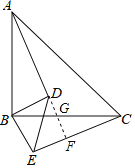
∵△ABD≌△CBE,
∵∠BAD=∠BCE,
又∵∠BGA=∠CGF,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目