题目内容
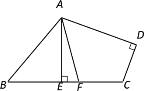
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有( )

A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
根据同角的余角相等求出∠BAD=∠C,再根据等角的余角相等可以求出∠AEF=∠AFE;根据等腰三角形三线合一的性质求出AG⊥EF.
∵∠BAC=90°,AD⊥BC,
∴∠C+∠ABC=90°,
∠BAD+∠ABC=90°,
∴∠BAD=∠C,故①正确;
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵∠ABE+∠AEF=90°,
∠CBE+∠BFD=90°,
∴∠AEF=∠BFD,
又∵∠AFE=∠BFD(对顶角相等),
∴∠AEF=∠AFE,故②正确;
∵∠ABE=∠CBE,
∴只有∠C=30°时∠EBC=∠C,故③错误;
∵∠AEF=∠AFE,
∴AE=AF,
∵AG平分∠DAC,
∴AG⊥EF,故④正确.
综上所述,正确的结论是①②④.
故选B.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目