ЬтФПФкШн
ЁОЬтФПЁПМзЁЂввСНШЫЗжБ№ЦяздааГЕКЭФІЭаГЕЃЌДгЭЌвЛЕиЕубиЯрЭЌЕФТЗЯпЧАЭљОрРы80kmЕФФГЕиЃЌЭМжаl1ЃЌl2ЗжБ№БэЪОМзЁЂввСНШЫРыПЊГіЗЂЕиЕФОрРыsЃЈkmЃЉгыааЪЛЪБМфtЃЈhЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЎЧыИљОнЭМЯѓНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзЁЂввСНШЫЫЕНДяФПЕФЕиНЯдчЃПдчЖрГЄЪБМфЃП
ЃЈ2ЃЉЗжБ№ЧѓМзЁЂввСНШЫааЪЛЙ§ГЬжаsгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЪдШЗЖЈЕБСНСОГЕЖМдкааЪЛЭОжаЃЈВЛАќРЈГіЗЂЕиКЭФПЕФЕиЃЉЪБЃЌtЕФШЁжЕЗЖЮЇЃЛВЂдкетвЛЪБМфЖЮФкЃЌЧѓtЮЊКЮжЕЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃП

ЁОД№АИЁПЃЈ1ЃЉввЕНДяФПЕФЕиНЯдчЃЌБШМздч2аЁЪБЃЛЃЈ2ЃЉМзЃКsЃН16tЃЛввЃК sЃН40tЉ40ЃЛЃЈ3ЃЉ1ЃМxЃМ3ЪБЃЌСНШЫОљааЪЛдкЭОжаЃЈВЛАќРЈЦ№ЕуКЭжеЕуЃЉЃЌ![]() ЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃЎ
ЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнКЏЪ§ЭМЯѓПЩвджБНгНтД№БОЬтЃЛ
ЃЈ2ЃЉИљОнЭМЯѓжаЕФЪ§ОнПЩвдЗжБ№ЧѓЕУl1КЭl2ЖдгІЕФБэДяЪНЃЛ
ЃЈ3ЃЉИљОнЭМЯѓПЩЕУЕБСНСОГЕЖМдкааЪЛЭОжаЃЈВЛАќРЈГіЗЂЕиКЭФПЕФЕиЃЉЪБЃЌtЕФШЁжЕЗЖЮЇЃЛИљОнЃЈ2ЃЉЕФНсТлЧѓГіСНжБЯпЕФНЛЕузјБъМДПЩЕУГіtЮЊКЮжЕЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃЎ
НтЃКЃЈ1ЃЉИљОнЭМЯѓПЩжЊЃЌввЕНДяФПЕФЕиНЯдчЃЌБШМздч2аЁЪБЃЌ
ЙЪД№АИЮЊЃКввЕНДяФПЕФЕиНЯдчЃЌБШМздч2аЁЪБЃЛ
ЃЈ2ЃЉИљОнЭМЯѓПЩжЊЃЌМзЕФЫйЖШЮЊЃК80ЁТ5ЃН16ЃЈkm/hЃЉЃЌ
Ёрl1ЖдгІЕФБэДяЪНЮЊsЃН16tЃЛ
ввЕФЫйЖШЮЊ80ЁТЃЈ3Љ1ЃЉЃН40ЃЈkm/hЃЉЃЌ
Щшl2ЖдгІЕФБэДяЪНЮЊsЃН40t+bЃЌАбЃЈ3ЃЌ80ЃЉДњШыЕУЃЌ40ЁС3+bЃН80ЃЌНтЕУbЃНЉ40ЃЌ
Ёрl2ЖдгІЕФБэДяЪНЮЊsЃН40tЉ40ЃЌ
ЙЪД№АИЮЊЃКМзЃКsЃН16tЃЛввЃК sЃН40tЉ40ЃЛ
ЃЈ3ЃЉгЩЭМЯѓПЩЕУЃК1ЃМxЃМ3ЪБЃЌСНШЫОљааЪЛдкЭОжаЃЈВЛАќРЈЦ№ЕуКЭжеЕуЃЉЃЎ
СЊСЂl1КЭl2ЃК![]() ЃЌНтЕУ
ЃЌНтЕУ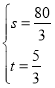 ЃЌ
ЃЌ
Ёр![]() ЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃЌ
ЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃЌ
ЙЪД№АИЮЊЃК1ЃМxЃМ3ЪБЃЌСНШЫОљааЪЛдкЭОжаЃЈВЛАќРЈЦ№ЕуКЭжеЕуЃЉЃЌ![]() ЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃЎ
ЪБЃЌФІЭаГЕааЪЛдкздааГЕЧАУцЃЎ