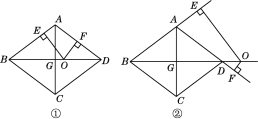
题目内容
【题目】如图,在![]() 中,
中,![]() ,AD、BD、CD分别平分
,AD、BD、CD分别平分![]() 的外角
的外角![]() ,内角
,内角![]() ,外角
,外角![]() ,以下结论:①
,以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论有__.
,其中正确的结论有__.

【答案】①③④
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF
=2∠DCF,根据三角形的内角和定理得出∠BAC+ABC+∠ACB=180°,根据三角形
外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理
即可判断各项
①∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确。
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②错误。
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
故③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,
∴∠ADB=∠DBC,
∵∠DCF=90°-![]() ∠ABC=90°-∠BDC=∠DBC+∠BDC
∠ABC=90°-∠BDC=∠DBC+∠BDC
∵∠ABC=90°-∠BDC=∠DBC+∠BDC,
∴∠BDC=90°-2∠DBC,
∠DBC=45°-![]() ∠BDC,④正确
∠BDC,④正确
故选:①③④.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目