题目内容
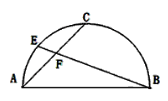
【题目】如图,直线L:![]() 交x轴与点A,交y轴与点B,点C在x轴正半轴上,且OC=2,点D在线段AC上,且∠CDB=∠ABC,过点C作BC的垂线,交BD的延长线与点E,并联结AE
交x轴与点A,交y轴与点B,点C在x轴正半轴上,且OC=2,点D在线段AC上,且∠CDB=∠ABC,过点C作BC的垂线,交BD的延长线与点E,并联结AE
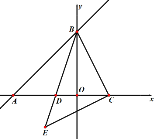
(1)求证:△CDB∽△CBA
(2)求点E的坐标
(3)若点P是直线CE上的一动点,联结DP若△DEP和△ABC相似,求点P的坐标
【答案】(1)见解析;(2)E(-2,-2);(3)![]() ,
,![]() .
.
【解析】
(1)直接由题目已知∠CDB=∠ABC和公共角∠BCA=∠BCA得出;
(2)先利用勾股定理,求出![]() ,由△CDB∽△CBA,得到
,由△CDB∽△CBA,得到![]() ,可求出CD的长度,找出D点的坐标,再利用B,D两点坐标,求出直线BD的关系式为
,可求出CD的长度,找出D点的坐标,再利用B,D两点坐标,求出直线BD的关系式为![]() ,设点E的坐标为(a,3a+4),根据△BCE是等腰直角三角形,利用勾股定理可得
,设点E的坐标为(a,3a+4),根据△BCE是等腰直角三角形,利用勾股定理可得![]() ,化简求值即可;
,化简求值即可;
(3)根据题意和(1)、(2)中的结果,利用分类讨论的方法可以求得点P的坐标.
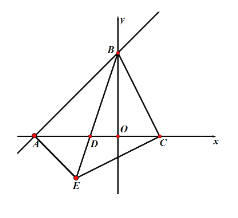
解:(1)∵∠CDB=∠ABC,∠BCA=∠BCA,
∴△CDB∽△CBA
(2)由(1)可知△CDB∽△CBA,
∴![]() ,
,
∴![]() ,
,
∵直线L:![]() 交x轴于点A,交y轴于点B,
交x轴于点A,交y轴于点B,
∴点A的坐标为(-4,0),点B的坐标为(0,4),
∴在Rt△AOB中,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴在Rt△OCB中,![]() ,
,
根据![]() ,
,
∴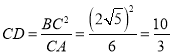 ,
,
∴![]()
即:![]() ,
,![]() ,
,
设过点B(0,4),![]() 的直线解析式为
的直线解析式为![]() ,
,
∴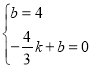 ,解之得:
,解之得:![]() ,
,
即直线BD的解析式为![]() ,
,
∵点E在直线BD上,
∴设点E的坐标为(a,3a+4),
∵OA=OB,∠AOB=90°,
∴∠BAO=∠BAC=45°,
∵△ABC∽△BDC,∠BAC=∠DBC,
∴∠DBC=45°,
∵BC⊥CE,
∴∠BCE=90°,
∴∠BEC=45°,
∴∠BEC=∠EBC,
∴BC=CE,
∵点B(0,4),点C(2,0),点E(a,3a+4),
∴![]()
解得,a=-2或a=0(舍去),
当a=-2时,3a+4=-2,
∴点E的坐标为(-2,-2),
(3)由(2)知,∠DEP=45°,∠BAC=45°,
当∠EDP=∠ABC时,△DEP与△ABC相似,
则:![]() ,
,
∵![]() ,AC=6,点D(
,AC=6,点D(![]() ,0),点E(-2,-2),
,0),点E(-2,-2),
∴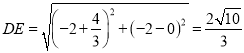 ,
,
∴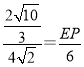 ,
,
解得,![]() ,
,
设过点E(-2,-2),C(2,0)的直线解析式为![]() ,
,
![]() ,解之得:
,解之得: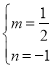 ,
,
即直线EC的解析式为![]() ,
,
∵点P在直线EC上,
∴设点P的坐标为(c,![]() ),
),
∵点E(-2,-2),![]() ,
,
解得,c=-4(舍去)或c=0,
∴当c=0时,![]() ,
,
即点P的坐标为(0,-1);
当∠EPD=∠ABC时,△DEP与△ABC相似,
则![]() ,
,
∵![]() ,AC=6,
,AC=6,![]() ,
,
∴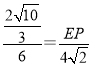 ,解得:
,解得:![]() ,
,
∵直线EC的解析式为![]() ,点P在直线EC上,
,点P在直线EC上,
∴设点P的坐标为(d,![]() ),
),
∵点E(-2,-2),![]() ,
,
∴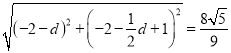 ,
,
解得:![]() (舍去)或
(舍去)或![]() ,
,
当![]() 时,
时,![]() ,
,
即点P的坐标为(![]() ,
,![]() );
);
由上可得,当△DEP与△ABC相似时,点P坐标是(0,-1)或
(![]() ,
,![]() ).
).