题目内容
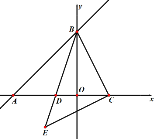
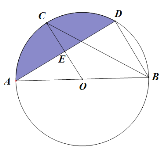
【题目】如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=8,∠CBD=30°,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1) 先由AB是圆O的直径可得∠ADB=90°,再运用平行线的性质可得OC⊥AD,再运用垂径定理即可求解;
(2) 用![]() -
-![]() 即可得.
即可得.
(1)证明:∵AB是圆O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
∴AE=ED;
(2)
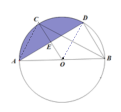
连接AC、OD
由(1)得OC⊥AD,
∴![]()
∴AC=CD
∵∠CBD=30°
∴∠COD=60°
∴∠AOC=∠COD=60°
∴∠AOD=120°
∵AB=8
∴OA=OD=4
∴BD=4
∴OE=![]() OC=2
OC=2
∴![]()
∴![]()
∵OC⊥AD
∴![]()
∴![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目