题目内容
【题目】如图,△ABC内接于⊙O,AB是直径,过点A作直线MN,且∠MAC=∠ABC.
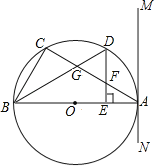
(1)求证:MN是⊙O的切线.
(2)设D是弧AC的中点,连结BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F.
①求证:FD=FG.
②若BC=3,AB=5,试求AE的长.
【答案】(1)见解析;(2)①见解析;②AE=1
【解析】
(1)由AB为直径知∠ACB=90°,∠ABC+∠CAB=90°.由∠MAC=∠ABC可证得∠MAC+∠CAB=90°,则结论得证;
(2)①证明∠BDE=∠DGF即可.∠BDE=90°﹣∠ABD;∠DGF=∠CGB=90°﹣∠CBD.因为D是弧AC的中点,所以∠ABD=∠CBD.则问题得证;
②连接AD、CD,作DH⊥BC,交BC的延长线于H点.证明Rt△ADE≌Rt△CDH,可得AE=CH.根据AB=BH可求出答案.
(1)证明:∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°;
∵∠MAC=∠ABC,
∴∠MAC+∠CAB=90°,即MA⊥AB,
∴MN是⊙O的切线;
(2)①证明:∵D是弧AC的中点,
∴∠DBC=∠ABD,
∵AB是直径,
∴∠CBG+∠CGB=90°,
∵DE⊥AB,
∴∠FDG+∠ABD=90°,
∵∠DBC=∠ABD,
∴∠FDG=∠CGB=∠FGD,
∴FD=FG;
②解:连接AD、CD,作DH⊥BC,交BC的延长线于H点.
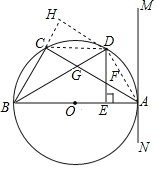
∵∠DBC=∠ABD,DH⊥BC,DE⊥AB,
∴DE=DH,
在Rt△BDE与Rt△BDH中,
![]() ,
,
∴Rt△BDE≌Rt△BDH(HL),
∴BE=BH,
∵D是弧AC的中点,
∴AD=DC,
在Rt△ADE与Rt△CDH中,
![]() ,
,
∴Rt△ADE≌Rt△CDH(HL).
∴AE=CH.
∴BE=AB﹣AE=BC+CH=BH,即5﹣AE=3+AE,
∴AE=1.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案