题目内容
【题目】在坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣3,0)和B(1,0),与y轴交于点C,
(1)求抛物线的表达式;
(2)若点D为此抛物线上位于直线AC上方的一个动点,当△DAC的面积最大时,求点D的坐标;
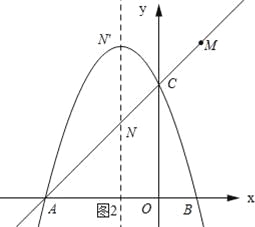
(3)设抛物线顶点关于y轴的对称点为M,记抛物线在第二象限之间的部分为图象G.点N是抛物线对称轴上一动点,如果直线MN与图象G有公共点,请结合函数的图象,直接写出点N纵坐标t的取值范围.
【答案】(1)y=﹣x2﹣2x+3;(2)D(﹣![]() ,
, ![]() );(3)当2<t≤4时,直线MN与函数图象G有公共点.
);(3)当2<t≤4时,直线MN与函数图象G有公共点.
【解析】试题分析:(1)设抛物线的解析式为y=a(x+3)(x﹣1),然后将a=﹣1代入即可求得抛物线的解析式;
(2)过点D作DE∥y轴,交AC于点E.先求得点C的坐标,然后利用待定系数法求得直线AC的解析式,设点D的坐标为![]() ,则E点的坐标为(x,x+3),于是得到DE的长(用含x的式子表示,接下来,可得到△ADC的面积与x的函数关系式,最后依据配方法可求得三角形的面积最大时,点D的坐标;
,则E点的坐标为(x,x+3),于是得到DE的长(用含x的式子表示,接下来,可得到△ADC的面积与x的函数关系式,最后依据配方法可求得三角形的面积最大时,点D的坐标;
(3)如图2所示:先求得抛物线的顶点坐标,于是可得到点M的坐标,可判断出点M在直线AC上,从而可求得点N的坐标,当点N′与抛物线的顶点重合时,N′的坐标为(﹣1,4),于是可确定出t的取值范围.
试题解析:(1)设抛物线的解析式为y=a(x+3)(x﹣1).
由题意可知:a=﹣1.
∴抛物线的解析式为y=﹣1(x+3)(x﹣1),即![]() ;
;
(2)如图所示:过点D作DE∥y轴,交AC于点E.
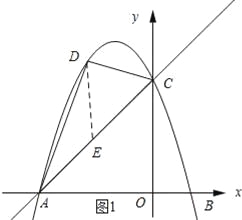
∵当x=0时,y=3,
∴C(0,3).
设直线AC的解析式为y=kx+3.
∵将A(﹣3,0)代入得:﹣3k+3=0,解得:k=1,
∴直线AC的解析式为y=x+3.
设点D的坐标为(x, ![]() ),则E点的坐标为(x,x+3).
),则E点的坐标为(x,x+3).
∴DE=![]() ﹣(x+3)=
﹣(x+3)=![]() .
.
∴△ADC的面积=![]() DEOA=
DEOA=![]() ×3×(
×3×(![]() )=
)=![]() .
.
∴当x=![]() 时,△ADC的面积有最大值.
时,△ADC的面积有最大值.
∴D![]() .
.
(3)如图2所示:
∵y=![]() =
=![]() ,
,
∴
∵点M与抛物线的顶点关于y轴对称,
∴M(1,4).
∵将x=1代入直线AC的解析式得y=4,
∴点M在直线AC上.
∵将x=﹣1代入直线AC的解析式得:y=2,
∴N(﹣1,2).
又∵当点N′与抛物线的顶点重合时,N′的坐标为(﹣1,4).
∴当2<t≤4时,直线MN与函数图象G有公共点.