题目内容
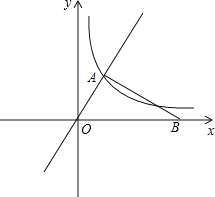
【题目】如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
(1)求证:CD是⊙O的切线;
(2)E为![]() 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=
的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=![]() ,BE=BG,EG=3
,BE=BG,EG=3![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OC,先证明∠OCB=∠CBD得到OC∥AD,再利用CD⊥AB得到OC⊥CD,然后根据切线的判定定理得到结论;
(2)解:连接OE交AB于H,如图,利用垂径定理得到OE⊥AB,再利用圆周角定理得到∠ABE=∠AFE,在Rt△BEH中利用正切可设EH=3x,BH=4x,则BE=5x,所以BG=BE=5x,GH=x,接着在Rt△EHG中利用勾股定理得到x2+(3x)2=(3![]() )2,解方程得x=3,接下来设⊙O的半径为r,然后在Rt△OHB中利用勾股定理得到方程(r-9)2+122=r2,最后解关于r的方程即可.
)2,解方程得x=3,接下来设⊙O的半径为r,然后在Rt△OHB中利用勾股定理得到方程(r-9)2+122=r2,最后解关于r的方程即可.
(1)证明:连接OC,如图,

∵BC平分∠OBD,
∴∠OBD=∠CBD,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OCB=∠CBD,
∴OC∥AD,
而CD⊥AB,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连接OE交AB于H,如图,
∵E为![]() 的中点,
的中点,
∴OE⊥AB,
∵∠ABE=∠AFE,
∴tan∠ABE=tan∠AFE=![]() ,
,
∴在Rt△BEH中,tan∠HBE=![]()
设EH=3x,BH=4x,
∴BE=5x,
∵BG=BE=5x,
∴GH=x,
在Rt△EHG中,x2+(3x)2=(3![]() )2,解得x=3,
)2,解得x=3,
∴EH=9,BH=12,
设⊙O的半径为r,则OH=r-9,
在Rt△OHB中,(r-9)2+122=r2,解得r=![]() ,
,
即⊙O的半径为![]() .
.

 口算能手系列答案
口算能手系列答案【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?