题目内容
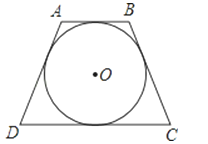
【题目】已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长.
【答案】60;18.
【解析】试题分析: (1)作AB⊥CD于E,BF⊥CD与F,因为⊙O为等腰梯形ABCD的内切圆,
根据切线长定理可得:AB+CD=AD+BC=20,因为AB∥CD,所以AE=6,所以等腰梯形ABCD的面积=![]() (AB+CD)AE=
(AB+CD)AE=![]() ×20×6=60,
×20×6=60,
(2)在Rt△ADE中,因为AD=10,AE=6,根据勾股定理可得DE![]() 8,因为梯形ABCD为等腰梯形,
8,因为梯形ABCD为等腰梯形,
所以CF=DE=8,根据(1)中AB+CD=20,AB=EF,所以8+8+2EF=20,解得EF=2,所以梯形的下底CD=8+2+8=18.
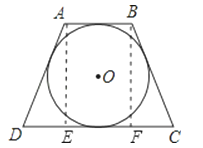
试题解析:作AB⊥CD于E,BF⊥CD与F,如图,
∵⊙O为等腰梯形ABCD的内切圆,
∴AB+CD=AD+BC=20,
∵AB∥CD,
∴AE=6,
∴等腰梯形ABCD的面积=![]() (AB+CD)AE=
(AB+CD)AE=![]() ×20×6=60,
×20×6=60,
在Rt△ADE中,
∵AD=10,AE=6,
∴DE=![]() 8,
8,
∵梯形ABCD为等腰梯形,
∴CF=DE=8,
而AB+CD=20,AB=EF,
∴8+8+2EF=20,解得EF=2,
∴梯形的下底CD=8+2+8=18.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目