题目内容
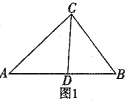
【题目】如图1,在△ABC中,∠ABC=45°,BC=7cm,AB=![]() cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
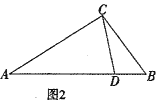
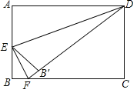
(1)如图2,过点P作PQ⊥BC,PQ交AB于点Q,以PQ为一边向右侧作矩形PQRS,若点R恰好在边AC上,且满足QR=2PQ.求BP得值.
(2)以点P为圆心,BP为半径作圆.
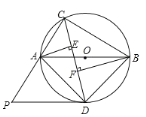
①如图3,当⊙P与边AC相切于点E时,求BP的值;
②随着BP的变化,⊙P与△ABC三边的公共点的个数也在变化,请直接写出公共点个数与对应的BP的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②当
;②当![]() 时,⊙P与AB和BC均有2个公共点,与AC无公共点;当
时,⊙P与AB和BC均有2个公共点,与AC无公共点;当![]() 时,⊙P与AB和BC均有2个公共点,与AC有1个公共点;当
时,⊙P与AB和BC均有2个公共点,与AC有1个公共点;当![]() 时,⊙P与AB、BC和AC均有2个公共点;当
时,⊙P与AB、BC和AC均有2个公共点;当![]() 时,⊙P与AB和AC有1个公共点,与BC有2个公共点;当
时,⊙P与AB和AC有1个公共点,与BC有2个公共点;当![]() 时,⊙P与AB和BC有1个公共点,与AC无个公共点.
时,⊙P与AB和BC有1个公共点,与AC无个公共点.
【解析】
(1)过点A做AD⊥BC,由AD是△ABC的高,∠ABC=45°,可得AD=BD,再由AB=![]() cm,即可得出AD的长,设BP=PQ=x,根据相似三角形的判定和性质列比例式求解;①过点A做AD⊥BC,连接PE,根据勾股定理求AC,根据AA定理判定△ADC∽△PEC,然后列比例式求解;
cm,即可得出AD的长,设BP=PQ=x,根据相似三角形的判定和性质列比例式求解;①过点A做AD⊥BC,连接PE,根据勾股定理求AC,根据AA定理判定△ADC∽△PEC,然后列比例式求解;
解:(1)过点A做AD⊥BC,交QR于点E
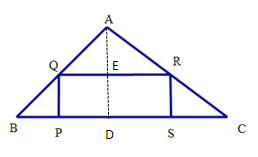
∵AD⊥BC,∠ABC=45°,
∴AD=BD=![]()
在矩形PQRS中RQ∥BC
∴△AQR∽△ABC
∴![]()
设BP=PQ=x,则QR=2x,AE=3-x
∴![]()
解得:x=![]()
∴BP=![]()
(2)①过点A做AD⊥BC,连接PE
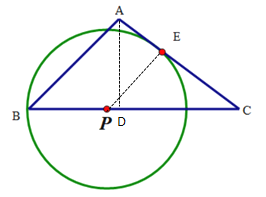
由(1)可知,BD=AD=3
∴CD=BC-BD=7-3=4
∴在Rt△ADC中,![]()
∵⊙P与边AC相切于点E
∴∠ADC=∠PEC=90°
又∵∠C=∠C
∴△ADC∽△PEC
∴![]()
设BP=PE=x
∴![]()
解得:x=![]()
∴BP=![]()
(3)由AB=![]() ,BC=7,(2)中BP=
,BC=7,(2)中BP=![]() 可知
可知
当![]() 时,⊙P与AB和BC均有2个公共点,与AC无公共点;
时,⊙P与AB和BC均有2个公共点,与AC无公共点;
当![]() 时,⊙P与AB和BC均有2个公共点,与AC有1个公共点;
时,⊙P与AB和BC均有2个公共点,与AC有1个公共点;
当![]() 时,⊙P与AB、BC和AC均有2个公共点;
时,⊙P与AB、BC和AC均有2个公共点;
当![]() 时,⊙P与AB和AC有1个公共点,与BC有2个公共点;
时,⊙P与AB和AC有1个公共点,与BC有2个公共点;
当![]() 时,⊙P与AB和BC有1个公共点,与AC无个公共点.
时,⊙P与AB和BC有1个公共点,与AC无个公共点.