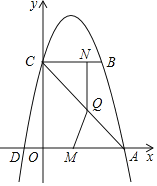题目内容
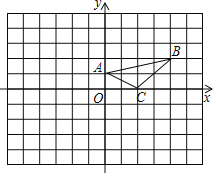
【题目】如图①,在平面直角坐标系中,ニ次函数![]() 的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
的图像与坐标轴交于A,B,C三点,其中点A的坐标为(-3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点0出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ
(1)填空:b=_, c=_;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
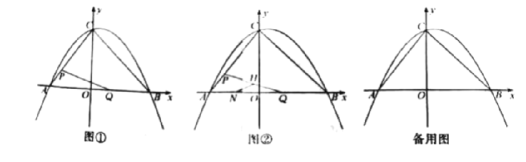
(3)如图2,点N的坐标为![]() ,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
,线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q`恰好落在线段BC上时,请直接写出点Q`的坐标
【答案】(1) ![]() ;(2) △APQ不可能是直角三角形,证明见解析;(3) Q′(
;(2) △APQ不可能是直角三角形,证明见解析;(3) Q′(![]() ,
,![]() ).
).
【解析】
(1)设抛物线的解析式为y=a(x+3)(x-4),将a=![]() 代入可得到抛物线的解析式,从而可确定出b、c的值
代入可得到抛物线的解析式,从而可确定出b、c的值
(2)连结QC.先求得点C的坐标,则PC=5-t,依据勾股定理可求得AC=5,CQ![]() =t
=t![]() +16,接下来,依据CQ
+16,接下来,依据CQ![]() -CP
-CP![]() =AQ
=AQ![]() -AP
-AP![]() 列方程求解即可
列方程求解即可
(3)连结:OP,取OP的中点R,连结RH,NR,延长NR交线段BC与点Q.首先依据三角形的中位线定理得到EH=![]() QO=
QO=![]() t,RH∥OQ,NR=
t,RH∥OQ,NR=![]() AP=
AP=![]() t,则RH=NR,接下来,依据等腰三角形的性质和平行线的性质证明NH是∠QNQ`的平分线,然后求得直线NR和BC的解析式,最后求得直线NR和BC的交点坐标即可
t,则RH=NR,接下来,依据等腰三角形的性质和平行线的性质证明NH是∠QNQ`的平分线,然后求得直线NR和BC的解析式,最后求得直线NR和BC的交点坐标即可
(1)设抛物线的解析式为y=a(+3)(x-4).将a=-![]() 代入得:
代入得:![]()
∴![]()
(2)在点P、Q运动过程中,△APQ不可能是直角三角形。
理由如下:连结QC
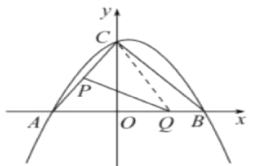
∵在点P、Q运动过程中,∠PAQ、∠PQA始终为锐角,
∴当△APQ是直角三角形时,则∠APQ=90°
将x=0代入抛物线的解析式得:y=4
∴C(0,4)
∵AP=OQ=t
∴PC=5-t
∵在Rt△AOC中,依据勾股定理得:AC=5,在Rt△COQ中,依据勾股定理可知: CQ![]() =t
=t![]() +16,
+16,
在Rt△CPQ中依据勾股定理可知:
PQ![]() =CQ
=CQ![]() -CP
-CP![]() ,在Rt△APQ中,AQ
,在Rt△APQ中,AQ![]() -AP
-AP![]() =PQ
=PQ![]()
∴CQ![]() -CP
-CP![]() =AQ
=AQ![]() -AP
-AP![]() ,即
,即
(3+t)![]() -t
-t![]() =t
=t![]() +16-(5-t)
+16-(5-t)![]() ,解得:t=4.5
,解得:t=4.5
∵由题意可知:0≤t≤4
∴t=4.5不和题意,即△APQ不可能是直角三角形。
(3)如图所示:连结:OP,取OP的中点R,连结RH,NR,延长NR交线段BC与点Q`
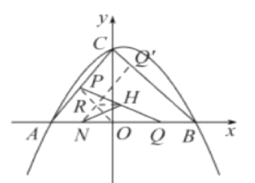
∵点H为PQ的中点,点R为OP的中点
∴EH=![]() QO=
QO=![]() t, RH∥OQ
t, RH∥OQ
∵A(-3,0),N(-![]() ,0)
,0)
∴点N为OA的中点
又∵R为OP的中点,
NR=![]() AP=
AP=![]() t
t
∴RH=NR,
∴∠RNH=∠RHN
∵RH∥OQ,
∴∠RHN=∠HNO
∴∠RNH=∠HNO,即NH是∠QNQ`的平分线.
设直线AC的解析式为y=mx+n,把点A(3,0)、C(0,4)
代入得:![]()
解得: ![]() ,n=4
,n=4
∴直线AC的表示为:y=![]()
同理可求得直线BC的表达式为y=-x+4
设直线NR的函数表达式为y=![]() 将点N的坐标代入得
将点N的坐标代入得![]()
,解得:S=2
直线NR的表述表达式为y=![]()
将直线NR和直线BC的表达式联立得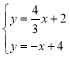
解得:x=![]() , y=
, y=![]() ,
,
∴Q`(![]() ,
,![]() )
)

【题目】某家庭记录了未使用节水龙头50天的日用水量(单位:m3)和使用了节木龙头50天的日用水量,得到频数分布表如下:
表1未使用节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 | 0.6≤x≤0.7 |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
表2使用了节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)估计该家庭使用节水龙头后,日用水量小于0.3 m3的概率;
(2)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在范围的组中值作代表.)