题目内容
如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的半径r1=2,⊙O2的半径r2=![]() .过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C.D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A.B,连接AP、BP、AC.DB,且AC与DB的延长线交于点E.
.过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C.D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A.B,连接AP、BP、AC.DB,且AC与DB的延长线交于点E.

(1)求证:![]() ;
;
(2)若PQ=2,试求∠E度数.
答案:
解析:
提示:
解析:
|
解答:(1)证明:∵⊙O1的半径r1=2,⊙O2的半径r2= ∴PC=4,PD=2 ∵CD⊥PQ, ∴∠PQC=∠PQD=90°, ∴PC.PD分别是⊙O1、⊙O2的直径, 在⊙O1中,∠PAB=∠PCD, 在⊙O2中,∠PBA=∠PDC, ∴△PAB∽△PCD, ∴ 即 (2)答:∠E的度数是75°. 解:在Rt△PCQ中,∵PC=2r1=4,PQ=2, ∴cos∠CPQ= ∴∠CPQ=60°, ∵在Rt△PDQ中,PD=2r2=2 ∴sin∠PDQ= ∴∠PDQ=45°, ∴∠CAQ=∠CPQ=60°,∠PBQ=∠PDQ=45°, 又∵PD是⊙O2的直径, ∴∠PBD=90°, ∴∠ABE=90°-∠PBQ=45° 在△EAB中,∴∠E=180°-∠CAQ-∠ABE=75° |
提示:
|
相交两圆的性质;三角形内角和定理;圆周角定理;相似三角形的判定与性质;解直角三角形. |

练习册系列答案
相关题目
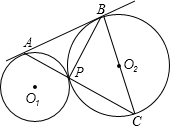 如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,
如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,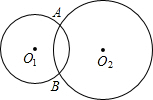 如图,⊙O1、⊙O2相交于点A、B,现给出4个命题:
如图,⊙O1、⊙O2相交于点A、B,现给出4个命题: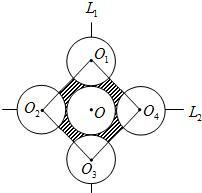 如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为
如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为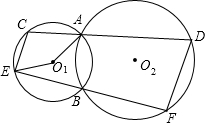 已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为
已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为 (1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )
(1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )