题目内容
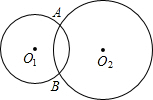 如图,⊙O1、⊙O2相交于点A、B,现给出4个命题:
如图,⊙O1、⊙O2相交于点A、B,现给出4个命题:(1)若AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,则AB2=BC•BD;
(2)连接AB、O1O2,若O1A=15cm,O2A=20cm,AB=24cm,则O1O2=25cm;
(3)若CA是⊙O1的直径,DA是⊙O2的一条非直径的弦,且点D、B不重合,则C、B、D三点不在同一条直线上;
(4)若过点A作⊙O1的切线交⊙O2于点D,直线DB交⊙O1于点C,直线CA交⊙O2于点E,连接DE,则DE2=DB•DC.
则正确命题的序号是
分析:(1)根据弦切角定理可以证明:∠BAD=∠C,∠BAC=∠D,则△ABD∽△CBA,从而证明结论;
(2)根据相交两圆的连心线垂直平分两圆的公共弦,再结合勾股定理,即可计算;
(3)根据直径所对的圆周角是直角,则∠ABC=90°,∠ABD≠90°,则∠CBD≠180°;
(4)根据切割线定理,得到DA2=DB•DC,所以只需证明DA=DE,即∠DAE=∠AED.
连接AB,根据弦切角定理和圆周角定理的推论,以及三角形的外角的性质,可以证明.
(2)根据相交两圆的连心线垂直平分两圆的公共弦,再结合勾股定理,即可计算;
(3)根据直径所对的圆周角是直角,则∠ABC=90°,∠ABD≠90°,则∠CBD≠180°;
(4)根据切割线定理,得到DA2=DB•DC,所以只需证明DA=DE,即∠DAE=∠AED.
连接AB,根据弦切角定理和圆周角定理的推论,以及三角形的外角的性质,可以证明.
解答: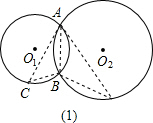 解:(1)∵AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,
解:(1)∵AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,
∴∠BAD=∠C,∠BAC=∠D,
∴△ABD∽△CBA,
∴
=
,
∴AB2=BC•BD;
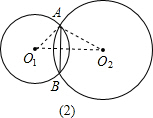 (2)∵O1O2垂直平分AB,
(2)∵O1O2垂直平分AB,
∴AC=BC=12,
根据勾股定理,得:
O1C=9,O2C=15,
∴O1O2=24;
 (3)∵CA是⊙O1的直径,DA是⊙O2的一条非直径的弦,
(3)∵CA是⊙O1的直径,DA是⊙O2的一条非直径的弦,
∴∠ABC=90°,∠ABD≠90°,
∴∠CBD≠180°,
∴C、B、D三点不在同一条直线上;
(4)连接AB,
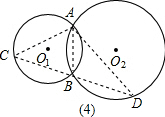 根据切割线定理,得DA2=DB•DC;
根据切割线定理,得DA2=DB•DC;
∵AD切⊙O1于A,
∴∠BAD=∠C,
又∵∠DAE=∠C+∠ADC,∠ABC=∠BAD+∠ADC,
∴∠DAE=∠ABC;
∵四边形ABDE是圆内接四边形,
∴∠ABC=∠E,
∴∠DAE=∠E,
∴DE=AD,
∴DE2=DB•DC.
故正确的有(1)(2)(3)(4).
 解:(1)∵AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,
解:(1)∵AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1的切线且交⊙O2于点D,∴∠BAD=∠C,∠BAC=∠D,
∴△ABD∽△CBA,
∴
| AB |
| BC |
| BD |
| AB |
∴AB2=BC•BD;
 (2)∵O1O2垂直平分AB,
(2)∵O1O2垂直平分AB,∴AC=BC=12,
根据勾股定理,得:
O1C=9,O2C=15,
∴O1O2=24;
 (3)∵CA是⊙O1的直径,DA是⊙O2的一条非直径的弦,
(3)∵CA是⊙O1的直径,DA是⊙O2的一条非直径的弦,∴∠ABC=90°,∠ABD≠90°,
∴∠CBD≠180°,
∴C、B、D三点不在同一条直线上;
(4)连接AB,
 根据切割线定理,得DA2=DB•DC;
根据切割线定理,得DA2=DB•DC;∵AD切⊙O1于A,
∴∠BAD=∠C,
又∵∠DAE=∠C+∠ADC,∠ABC=∠BAD+∠ADC,
∴∠DAE=∠ABC;
∵四边形ABDE是圆内接四边形,
∴∠ABC=∠E,
∴∠DAE=∠E,
∴DE=AD,
∴DE2=DB•DC.
故正确的有(1)(2)(3)(4).
点评:连接公共弦是相交两圆常见的辅助线之一.综合运用切割线定理、弦切角定理、圆周角定理的推论.掌握相似三角形的性质和判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
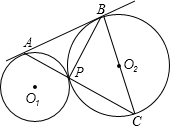 如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,
如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,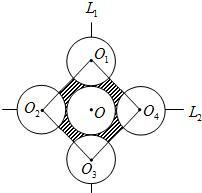 如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为
如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为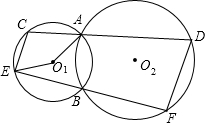 已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为
已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为 (1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )
(1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )