题目内容
 (1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )
(1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )分析:根据相交线定理以及相且两圆的性质得出两圆直径,进而得出答案即可.
解答: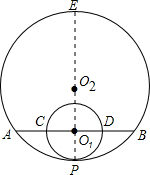 解:圆O1与圆O2内切于点P,O1,O2,P在一直线上,此直线与圆O2的另一交点设为E.
解:圆O1与圆O2内切于点P,O1,O2,P在一直线上,此直线与圆O2的另一交点设为E.
∴O1A•O1B=O1P•O1E,
∵若AC:CD:BD=3:4:2,⊙O2的弦AB经过⊙O1的圆心O1,
∴O1A:O1B=5:4,
设O1A=5x,则O1B=4x,CO1=2x,
∴O1E=
=10x,
∴圆O1与圆O2的直径分别为:4x,12x,
∴圆O1与圆O2的直径之比为:
=
.
故选:D.
 解:圆O1与圆O2内切于点P,O1,O2,P在一直线上,此直线与圆O2的另一交点设为E.
解:圆O1与圆O2内切于点P,O1,O2,P在一直线上,此直线与圆O2的另一交点设为E.∴O1A•O1B=O1P•O1E,
∵若AC:CD:BD=3:4:2,⊙O2的弦AB经过⊙O1的圆心O1,
∴O1A:O1B=5:4,
设O1A=5x,则O1B=4x,CO1=2x,
∴O1E=
| 5x•4x |
| 2x |
∴圆O1与圆O2的直径分别为:4x,12x,
∴圆O1与圆O2的直径之比为:
| 4x |
| 12x |
| 1 |
| 3 |
故选:D.
点评:此题主要考查了相切两圆的性质以及相交弦定理,根据已知得出O1A•O1B=O1P•O1E是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1998•南京)如图,圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是( )
(1998•南京)如图,圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是( ) (1998•南京)如图,用铁皮做一个圆锥形的烟囱帽,它的底面直径是80cm,高是30cm,不计加工余料,则需用铁皮的面积最少是( )
(1998•南京)如图,用铁皮做一个圆锥形的烟囱帽,它的底面直径是80cm,高是30cm,不计加工余料,则需用铁皮的面积最少是( )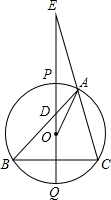 (1998•南京)已知:如图,△ABC内接于⊙O,过圆心O作BC的垂线交⊙O于点P、Q,交AB于点D,QP、CA的延长线交于点E.求证:OA2=OD•OE.
(1998•南京)已知:如图,△ABC内接于⊙O,过圆心O作BC的垂线交⊙O于点P、Q,交AB于点D,QP、CA的延长线交于点E.求证:OA2=OD•OE.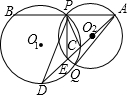 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且