题目内容
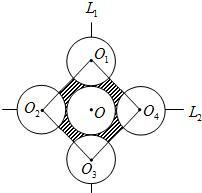 如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为
如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为分析:由图可知,阴影部分的面积等于正方形O1O2O3O4的面积减去两个圆的面积.由于O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,可据此求出正方形的对角线长,即可得出正方形的边长.然后根据正方形和圆的面积计算方法分别求出各自的面积,即可得出阴影部分的面积.
解答:解:∵⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切;
∴O1O3=O2O4=8cm,即O1O2=4
cm.
∴S阴影=S正方形O1O2O3O4-2S⊙O=32-2×4π=32-8π(cm2).
∴O1O3=O2O4=8cm,即O1O2=4
| 2 |
∴S阴影=S正方形O1O2O3O4-2S⊙O=32-2×4π=32-8π(cm2).
点评:本题考查了圆与圆的位置关系、正方形的性质和面积公式、圆的面积公式等知识点.

练习册系列答案
相关题目
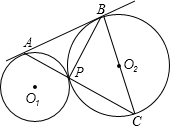 如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,
如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,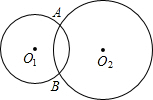 如图,⊙O1、⊙O2相交于点A、B,现给出4个命题:
如图,⊙O1、⊙O2相交于点A、B,现给出4个命题: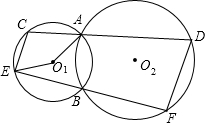 已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为
已知:如图,⊙O1和⊙O2相交于A、B两点,经过A的直线CD与⊙O1交于点C、与⊙O2交于点D,经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F,连接CE、DF.若∠AO1E=100°,则∠D的度数为 (1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )
(1998•南京)如图,⊙O1和⊙O2内切于点P,⊙O2的弦AB经过⊙O1的圆心O1,交⊙O1于点C、D,若AC:CD:BD=3:4:2,则⊙O1与⊙O2的直径之比为( )