题目内容
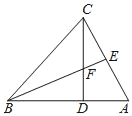
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE与BD交于点A.求证:
(1)BF=AC;
(2)BE是AC的中垂线;
(3)若AD=2,求AB的长.
【答案】(1)见解析;(2)见解析;(3)4+2![]() .
.
【解析】
(1)由 CD⊥AB,BE⊥AC,可得BDF=∠ADC=∠AEB=90°,DBF=∠DCA,继而证明出△BDF≌△CDA可得结论;
(2) BE平分∠ABC,可证∠A=∠BCA,BC=BA ,CE=EA可得结论;
(3) 由(1)BDF≌△CDA,可得各边的长,可求出AB的长.
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠BDF=∠ADC=∠AEB=90°,
∵∠DBF+∠A=90°,∠DCA+∠A=90°,
∴∠DBF=∠DCA,
∵BD=CD,
∴△BDF≌△CDA(SAS),
∴BF=AC.
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠BEA=∠BEC=90°,
∴∠A+∠ABE=90°,∠BCA+∠CBE=90°,
∴∠A=∠BCA,
∴BC=BA,
∵BE⊥AC,
∴CE=EA,
∴BE是AC的中垂线.
(3)解:连接AF.

∵△BDF≌△CDA,
∴AD=DF=2,AF=2![]() ,
,
∵BE垂直平分AC,
∴CF=AF=2![]() ,
,
∴BD=CD=2+2![]() ,
,
∴AB=BD+AD=4+2![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目