��Ŀ����
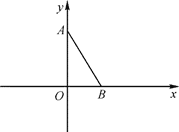
����Ŀ����ͼ��ƽ��ֱ������ϵ xOy �У���֪�� A(0��3)���� B(![]() ��0)������ AB��������ƽ ����һ�� C������ABC ���� AB Ϊ���ĵ���������ʱ���Ƶ� C ���߶� AB �ġ��ȳ��㡱
��0)������ AB��������ƽ ����һ�� C������ABC ���� AB Ϊ���ĵ���������ʱ���Ƶ� C ���߶� AB �ġ��ȳ��㡱
(1)�ڵ� C1 (��2�� ![]() )���� C2 (0����2)���� C3 (
)���� C2 (0����2)���� C3 (![]() ��
�� ![]() )�У��߶� AB �ġ��ȳ��㡱�ǵ�______________��
)�У��߶� AB �ġ��ȳ��㡱�ǵ�______________��
(2)���� D( m �� n )���߶� AB �ġ��ȳ��㡱���ҡ�DAB��60���� m �� n ��ֵ��
���𰸡���1��C1 ��C3����2��![]() ��
��![]() .
.
�������������������1�����ù��ɶ����ֱ���������ε������߳����ж��Ƿ�����ABΪ���ĵ��������Σ���2��������������ۣ��ٵ���D��y�����ʱ���ڵ���D��y���Ҳ�ʱ����ϵȳ���Ķ���ֱ�����������m��n��ֵ����.
���������
�⣺(1) C1 (��2��3+2![]() )��AO=3��BO=
)��AO=3��BO=![]() ��
��
��C1D��x�ύ�ڵ�D����C1E��y�ύ�ڵ�E��
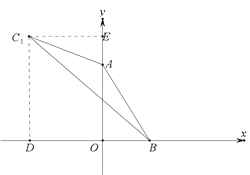
��C1D=3+2![]() ��C1E=2��
��C1E=2��
�ɹ��ɶ����ɵã�AB=2![]() ��AC1=2
��AC1=2![]() ��
��
��C1���߶�AB�ĵȳ��㣻
ͬ����֤��C3���߶�AB�ĵȳ��㣻
��2����ͼ1��
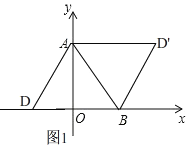
��Rt��AOB��OA=3��OB=![]() ��
��
��AB=2![]() ��tan��OAB=
��tan��OAB=![]() ��
��
���OAB��30����
�ٵ���D��y�����ʱ��
�ߡ�DAB��60����
���DAO����DAB����BAO= 30����
�ߵ�D( m��n )���߶�AB�����ȳ�������
��AD=AB��
��D��![]() ��0����
��0����
��m=![]() ��n=0��
��n=0��
�ڵ���D��y���Ҳ�ʱ��
�ߡ�DAB��60����
���DAO����BAO+��DAB= 90����
��n=3,
�ߵ�D( m��n )���߶�AB�����ȳ�������
��AD=AB=2![]() ��
��
��m=2![]() .
.
��m=2![]() ��n=3.
��n=3.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�


