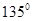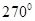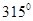题目内容
如图,已知∠AOB以O为圆心,以任意长为半径作弧,分别交OA、OB于F、E两点,再分别以E、F为圆心,大于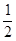 EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。

(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证△FMO≌△FMD.
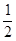 EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证△FMO≌△FMD.
(1)32°;(2)根据角平分线的性质结合平行线的性质得到∠A0D=∠ODF,再根据垂直的定义可得∠OMF=∠DMF,再结合公共边即可证得结论.
试题分析:(1)先根据平行线的性质求得∠A0B的度数,再根据角平分线的性质求解即可;
(2)根据角平分线的性质结合平行线的性质得到∠A0D=∠ODF,再根据垂直的定义可得∠OMF=∠DMF,再结合公共边即可证得结论.
(1)∵OB∥FD,
∴∠0FD+∠A0B=18O°,
又∵∠0FD=116°,
∴∠A0B=180°-∠0FD=180°-116°=64°,
由作法知,0P是∠A0B的平分线,
∴∠D0B=
 ∠A0B=32°;
∠A0B=32°;(2)∵0P平分∠A0B,
∴∠A0D=∠D0B,
∵0B∥FD,
∴∠D0B=∠ODF,
∴∠A0D=∠ODF,
又∵FM⊥0D,
∴∠OMF=∠DMF,
在△MFO和△MFD中,
∵∠OMF=∠DMF,∠A0D=∠ODF, FM=MF,
∴△MFO≌△MFD
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,再中考中极为重要,要熟练掌握.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
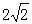 .求四边形
.求四边形 的面积.
的面积.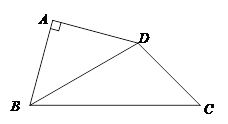
 在同一直线上,
在同一直线上, ∥
∥ ,且
,且 ,
, ,求证:
,求证: ∥
∥ .
.
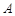 、
、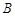 、
、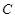 三点均在
三点均在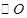 上,且
上,且 是等边三角形.
是等边三角形.
 是
是 上一点,连接
上一点,连接 、
、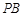 、
、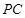 .探究
.探究
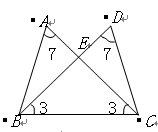



 为
为 的三边,则
的三边,则 ______
______ (填“>,=,<”).
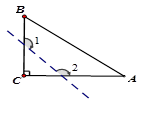
(填“>,=,<”).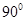 ,若沿图中虚线剪去∠C,则 ∠1+∠2等于 ( )
,若沿图中虚线剪去∠C,则 ∠1+∠2等于 ( )