题目内容
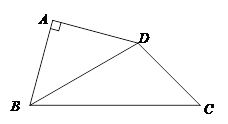
如图,四边形ABCD中,AB = AD,∠BAD=90°,∠CBD=30°,∠BCD=45°,
若AB=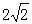 .求四边形
.求四边形 的面积.
的面积.
若AB=
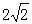 .求四边形
.求四边形 的面积.
的面积.
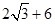
试题分析:解:过D做DM⊥BC于点M。
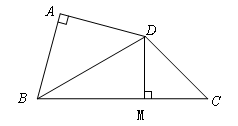
已知AB=AD。Rt△ABD和Rt△CDM为等腰直角三角形。
Rt△ABD中BD=
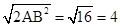 。在Rt△BDM中,∠CBD=30°,则DM=2.
。在Rt△BDM中,∠CBD=30°,则DM=2.BM=

所以Rt△CDM中,CM=DM=2.所以S△BCD=

S△ABD=

则四边形ABCD面积=
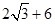
点评:本题难度中等,主要考查学生对几何图形面积求解和勾股定理知识点的掌握。

练习册系列答案
相关题目
 .
.
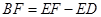 ;
; ,求
,求 的度数.
的度数. (结果保留根号的形式).
(结果保留根号的形式).
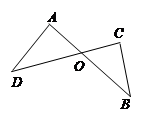
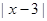 , 一条直角边的长是
, 一条直角边的长是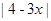 , 那么当另一条直角边达到最大时, 这个直角三角形的周长的范围大致在 ( )
, 那么当另一条直角边达到最大时, 这个直角三角形的周长的范围大致在 ( )
 则点
则点 到
到 的距离是_______
的距离是_______ 。
。
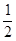 EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D。