Question

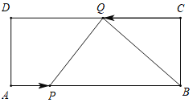
【题目】为了充分利用空间，在确定公园的设计方案时，准备利用公园的一角∠MON两边为边，用总长为16m的围栏在公园中围成了如图所示的①②③三块区域，其中区域①为直角三角形，区城②③为矩形，而且这三块区城的面积相等．

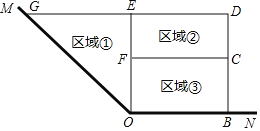
（1）设OB的长度为xm，则OE+DB的长为　 　m．

（2）设四边形OBDG的面积为ym2，求y与x之间的函数关系式；

（3）x为何值时，y有最大值？最大值是多少？

Answer 1

【答案】（1）16－3x;（2）y=﹣x2+12x (0＜x＜)；（3）当x＝时，y有最大值，最大值是16平方米

【解析】

（1）根据三角形和矩形的面积得到EGOE=CFEF=CFOF，得到EG=DE=CF=OB=x，于是得到结论；（2）由（Ⅰ）知OE+DB=16-3x，得到OE=DB=8-1.5x，根据矩形的面积公式即可得到结论；（3）根据二次函数的性质即可得到结论．

解：（1）由题意得，S△OEG＝S矩形CDEF＝S矩形OBCF，

∴EGOE＝CFEF＝CFOF，

∴EF＝OF＝OE，

∴EGOE＝OECF，

∴EG＝DE＝CF＝OB＝xm，

∴OE+DB＝（16﹣3x）m，

故答案为：（16﹣3x）．

（2）由（1）知OE+DB＝16﹣3x，

∴OE＝DB＝8﹣1.5x，

∴y＝，

∵

∴0＜x＜．

（3）∵y＝，

∵﹣＜0，且0＜x＜，

∴抛物线开口向下

∴当x＝时，y有最大值，最大值是16平方米．