题目内容
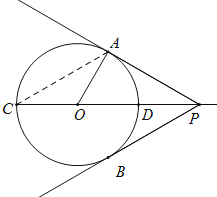
【题目】如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA,PB,切点分别为点A,B.

(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;
(2)填空:
①当DP= cm时,四边形AOBD是菱形;
②当DP= cm时,四边形AOBP是正方形.
【答案】(1)证明见解析;(2)1;![]() -1.
-1.
【解析】
试题分析:(1)利用切线的性质可得OC⊥PC.利用同弧所对的圆周角等于圆心角的一半,求得∠ACP=30°,从而求得.
(2)①要使四边形AOBD是菱形,则OA=AD=OD,所以∠AOP=60°,所以OP=2OA,DP=OD.
②要使四边形AOBP是正方形,则必须∠AOP=45°,OA=PA=1,则OP=![]() ,所以DP=OP-1.
,所以DP=OP-1.
试题解析:(1)连接OA,AC
∵PA是⊙O的切线,
∴OA⊥PA,
在Rt△AOP中,∠AOP=90°-∠APO=90°-30°=60°,
∴∠ACP=30°,
∵∠APO=30°
∴∠ACP=∠APO,
∴AC=AP,
∴△ACP是等腰三角形.
(2)①DP=1,理由如下:
∵四边形AOBD是菱形,
∴OA=AD=OD,
∴∠AOP=60°,
∴OP=2OA,DP=OD.
∴DP=1,
②DP=![]() -1,理由如下:
-1,理由如下:
∵四边形AOBP是正方形,
∴∠AOP=45°,
∵OA=PA=1,OP=![]() ,
,
∴DP=OP-1
∴DP=![]() -1.
-1.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
【题目】红星养猪场400头猪的质量(质量均为整数千克)频率分布如下,其中数据不在分点上,从中任选一头猪,质量在65kg以上的概率是___________.
组别 | 频数 | 频率 |
46 ~ 50 | 40 | |
51 ~ 55 | 80 | |
56 ~ 60 | 160 | |
61 ~ 65 | 80 | |
66 ~ 70 | 30 | |
71~ 75 | 10 |



