题目内容
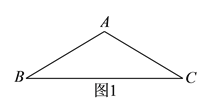
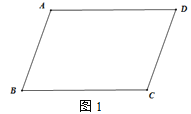
【题目】如图1,已知AD∥BC,∠B=∠D.
(1)求证:AB∥CD;
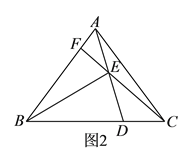
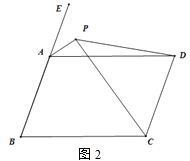
(2)如图2,点E为BA延长线上一点,∠EAD与∠BCD的角平分线交于点P.
①求∠APC的度数;
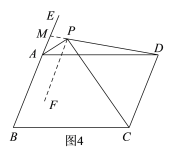
②连接DP,若∠PDC=750,则∠DPC-![]() ∠B=________.
∠B=________.
【答案】90°
【解析】
(1)根据平行线的性质和判定结合已知条件进行分析证明即可;
(2)①如图3,过点P作PF∥AB,结合已知条件易得∠EAP=∠APF,∠DCP=∠CPF,从而可得∠APC=∠EAP+∠DCP,由已知易得∠EAD=∠B,∠B+∠BCD=180°,进而可得∠EAD+∠BCD=180°,结合AP平分∠EAD,CP平分∠BCD即可得到∠APC=∠EAP+∠DCP=90°;②如图4,延长DP交BA的延长线于点M,由已知易得I、∠MPA+∠APF=75°,由∠APC=90°可得II、∠MPA+∠DPC=90°,再证∠APF=![]() ∠B,即可由I-II得到所求结果.
∠B,即可由I-II得到所求结果.
(1)∵AD∥BC,
∴∠ A+∠ B=180°,
∵∠ B=∠ D,即∠ A+∠ D =180°,
∴ AB∥CD;
(2)①过点P作直线PF∥AB,
∵在平行四边形ABCD中,AB∥CD,AD∥BC,
∴∠EAD=∠B,∠B+∠BCD=180°,AB∥PF∥CD,
∴∠EAD+∠BCD=180°,
∵AP平分∠EAD,CP平分∠BCD,
∴∠EAP=![]() ∠EAD,∠DCP=
∠EAD,∠DCP=![]() ∠BCD,
∠BCD,
∴∠EAP+∠DCP=![]() (∠EAD+∠BCD)=90°,
(∠EAD+∠BCD)=90°,
∵AB∥PF∥CD,
∴∠APF=∠EAP,∠CPF=∠DCP,
∴∠APC=∠APF+∠CPF=∠EAP+∠DCP=90°,即∠APC=90°;
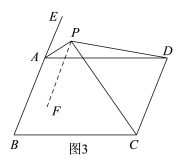
②如图4,延长DP交BA的延长线于点M,
∵AB∥PF∥CD,
∴∠APF=∠EAP=![]() ∠EAD=
∠EAD=![]() ∠B,∠MPA+∠APF=∠MPF=∠PDC=75°,
∠B,∠MPA+∠APF=∠MPF=∠PDC=75°,
∵∠APC=90°,
∴∠MPA+∠DPC=90°,
∴(∠MPA+∠DPC)-(∠MPA+∠APF)=90°-75°=15°,
∴∠DPC-∠APF=15°,
∴∠DPC-![]() ∠B=15°.
∠B=15°.