题目内容
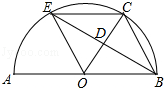
【题目】如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC. 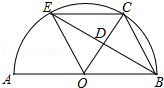
(1)求证:△BDO≌△EDC.
(2)若OB=6,则四边形OBCE的面积为 .
【答案】
(1)证明:∵∠COB=60°且OB=OC,
∴△BOC为等边三角形,∠OBC=60°,
又∵点D是OC的中点,
∴OD=CD,∠OBD= ![]() =30°,
=30°,
又∵点C是半圆上一点且∠COB=60°,
∴∠CEB= ![]() =30°,
=30°,
∴∠OBD=∠CEB,
在△BDO与△EDC中,
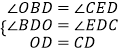 ,
,
∴△BDO≌△EDC(AAS);
(2)18 ![]()
【解析】∵∴△BDO≌△EDC, ∴EC=OB,
∵△OBC是等边三角形,
∴OB=BC=EC=EO,
∴四边形OBCE是菱形,
∴S菱形OBCE= ![]() OCEB=
OCEB= ![]() 66
66 ![]() =18
=18 ![]() .
.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半).

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目