Question

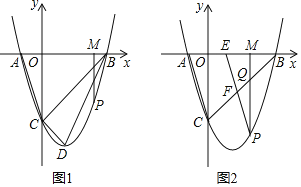
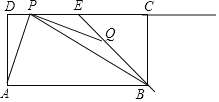
【题目】如图，在正方OABC中，点B的坐标是（4，4），点E、F分别在边BC、BA上，.若，则点F的纵坐标是（　　）

A.1B.C.2D.

Answer 1

【答案】B

【解析】

如图连接EF，延长BA使得AM=CE，则△OCE≌△OAM．先证明△OFE≌△FOM，推出EF=FM=AF+AM=AF+CE，设AF=x，在Rt△EFB中利用勾股定理列出方程即可解决问题．

如图连接EF，延长BA使得AM=CE，则△OCE≌△OAM．

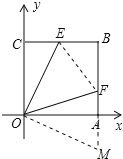
∴OE=OM，∠COE=∠MOA，

∵∠EOF=45°，

∴∠COE+∠AOF=45°，

∴∠MOA+∠AOF=45°，

∴∠EOF=∠MOF，
在△OFE和△OFM中，

，

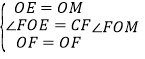∴△OFE≌△FOM，

∴EF=FM=AF+AM=AF+CE，设AF=x,

∵CE=，

∴EF=2+x，EB=2，FB=4-x，

∴（2+x）2=22+（4-x）2，

∴x=，

∴点F的纵坐标为，

故选B．