题目内容
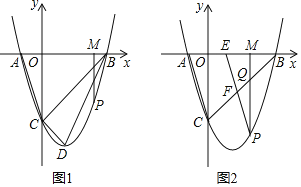
【题目】如图1,抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,﹣3),抛物线顶点为D,连接AC,BC,CD,BD,点P是x轴下方抛物线上的一个动点,作PM⊥x轴于点M,设点M的横坐标为m.
(1)求抛物线的解析式及点D的坐标;
(2)试探究是否存在这样的点P,使得以P,M,B为顶点的三角形与△BCD相似?若存在,请求出点P的坐标;若不存在,请说明理由;
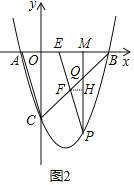
(3)如图2,PM交线段BC于点Q,过点P作PE∥AC交x轴于点E,交线段BC于点F,请用含m的代数式表示线段QF的长,并求出当m为何值时QF有最大值.
【答案】(1)y=x2﹣2x﹣3,(1,﹣4);(2)见解析;(3)见解析.
【解析】
(1)设抛物线解析式为:y=a(x+1)(x﹣3), 将C(0,-3),代入可求出解析式,根据抛物线的顶点坐标公式求出D点即可.
(2)由(1)可得BC=3![]() ,CD=
,CD=![]() ,BD=
,BD=![]() ,△BCD是直角三角形,∠BCD=90°,再分情况讨论:①当△PMB∽△BCD时,得点P(2,﹣3);②当△BMP∽△BCD时,点P的坐标为(﹣
,△BCD是直角三角形,∠BCD=90°,再分情况讨论:①当△PMB∽△BCD时,得点P(2,﹣3);②当△BMP∽△BCD时,点P的坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)设QF为y,作FH⊥PM于点H,先证明△FHP∽△AOC,得出PQ=![]() =2
=2![]() y,根据点B、C的坐标得到直线BC的表达式为:y=x﹣3,设点P(m,m2﹣2m﹣3),点Q(m,m﹣3),求出PQ=﹣m2+3m,即可解答.
y,根据点B、C的坐标得到直线BC的表达式为:y=x﹣3,设点P(m,m2﹣2m﹣3),点Q(m,m﹣3),求出PQ=﹣m2+3m,即可解答.
解:(1)设抛物线解析式为:y=a(x+1)(x﹣3),
将C(0,-3),代入可得:﹣3a=﹣3,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3,
根据顶点坐标公式得出D的坐标为![]()
∴点D的坐标为(1,﹣4);
(2)由(1)知,点B、C、D的坐标分别为(3,0)、(0,﹣3)、(1,﹣4),
则BC=3![]() ,CD=
,CD=![]() ,BD=
,BD=![]() ,
,
则△BCD是直角三角形,∠BCD=90°,
①当△PMB∽△BCD时,
则∠MPB=∠DBC,即:tan∠MPB=tan∠DBC=![]() ,
,
∵点M(m,0),则点P(m,m2﹣2m﹣3),
tan∠MPB=![]() ,
,
解得:m=2或3(舍去3),
故点P(2,﹣3);
②当△BMP∽△BCD时,
同理可得:点P(﹣![]() ,﹣
,﹣![]() );
);
故点P的坐标为:(2,﹣3)或(﹣![]() ,﹣
,﹣![]() );
);
(3)设QF为y,作FH⊥PM于点H,
∵OB=OC,∴∠OCB=∠OBC=45°
则FH=QH=![]() y,
y,
∵PE∥AC,PM∥OC,则∠PEM=∠HFP=∠CAO,
∴△FHP∽△AOC,
则PH=3FH=![]() y,
y,
∴PQ=![]() =2
=2![]() y,
y,
根据点B、C的坐标求出直线BC的表达式为:y=x﹣3,
则点P(m,m2﹣2m﹣3),点Q(m,m﹣3),
所以PQ=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,即:2![]() y=﹣m2+3m,
y=﹣m2+3m,
则y=![]() ,.
,.
∴当m=![]() 时,QF有最大值.
时,QF有最大值.

 53天天练系列答案
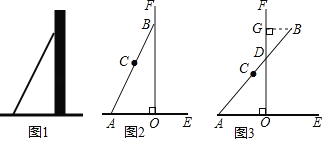
53天天练系列答案【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
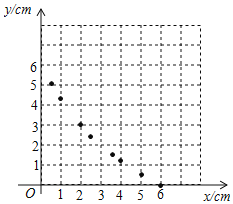
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.