题目内容
【题目】在平面直角坐标系中,四边形![]() 的矩形,点
的矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,直线
,直线![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
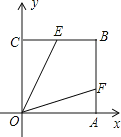
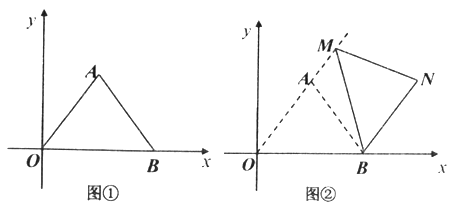
(Ⅰ)如图①,当矩形![]() 的顶点
的顶点![]() 落在
落在![]() 轴正半轴上时,
轴正半轴上时,
(1)求证:![]() ;
;
(2)求点![]() 的坐标.
的坐标.
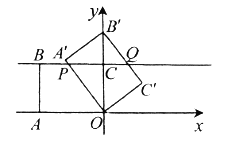
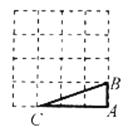
(Ⅱ)如图②,当矩形![]() 的顶点
的顶点![]() 落在直线
落在直线![]() 上时,
上时,
(1)求证:![]() .
.
(2)求点![]() 的坐标.
的坐标.
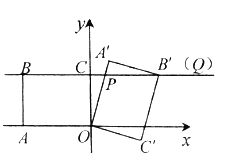
(Ⅲ)在矩形![]() 旋转过程中,当
旋转过程中,当![]() 时,若
时,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
【答案】(Ⅰ)(1)见解析;(2)点![]() 的坐标为
的坐标为![]() ; (Ⅱ)(1)见解析;(2)点
; (Ⅱ)(1)见解析;(2)点![]() 的坐标为
的坐标为![]() ;(Ⅲ)点
;(Ⅲ)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(Ⅰ)(1)由题意得∠B’CQ=∠C’即可求解;
(2)由题可得OA=8,OC=6. B’C’=BC=8,OC’=OC=6;由(1)知△B’CQ∽△B’C’O即可求解;
(Ⅱ)(1)由题意知A’B’=AB=OC,∠BCO=∠B’CO=∠A’=90,易得三角形全等;
(2)设CP=x,由(1)知△PCO≌△PA’B’,易得CP长即可求出P点坐标;
(3)分情况讨论:1°当P在BQ上时,由勾股定理易得PC长度即可求解;
2°当P在QB延长线上时,由勾股定理易得PC长度,即可求解.
(Ⅰ)(1)证明:根据题意,知∠B’CQ=∠BCO=90°,∠BCO=∠C’=90°,
∴∠B’CQ=∠C’=90°.
又∵∠QB’C=∠OB’C’
∴△B’CQ∽△B’C’O.
(2)解:∵点A(-8,0)C(0,6),∴OA=8,OC=6.
∵四边形OABC是矩形,∴BC=OA=8.
根据题意,知B’C’=BC=8,OC’=OC=6.
∴OB’=10,B’C=OB’-OC=4.
由(1)知△B’CQ∽△B’C’O,∴![]() ,即
,即![]() .∴CQ=3.
.∴CQ=3.
∴点Q的坐标为(3,6).
(Ⅱ)(1)证明:由题意知A’B’=AB=OC,∠BCO=∠B’CO=∠A’=90°,
又∵∠CPO=∠A’PB’∴ △PCO≌△PA’B’.
(2)解:根据题意,知A’O=AO=8.
设CP=x,由(1)知△PCO≌△PA’B’,
∴A’P=CP=x,A’B’=OC=6,PB’=PO=A’O-A’P=8-x.
在Rt△PA’B’中,![]() ,即
,即![]() ,
,
解得x=![]() ,∴CP=
,∴CP=![]() .
.
∴点P的坐标为(![]() ,6).
,6).
(Ⅲ)对于△PQO,PQ边上的高CO等于PO边上的高C’O
设BP=n
1°当P在BQ上时,∵BQ=2BP∴BP=PQ=n
在Rt△PCO中,由勾股定理得![]() 解得
解得![]()
∴PC=BC-BP=8-![]() =
=![]() 故P点坐标为(
故P点坐标为(![]() ,6)
,6)
2°当P在QB的延长线上时,∵BQ=2BP∴PQ= 3BP=3n
在Rt△PCO中,由勾股定理得![]() 解得
解得![]() 或
或![]() (舍)
(舍)
∴PC=BC+BP=8+![]() =
=![]() 故P点坐标为(-9-
故P点坐标为(-9-![]() ,6)
,6)
综上所述,点P的坐标为(-9-![]() ,6)或(
,6)或(![]() ,6).
,6).

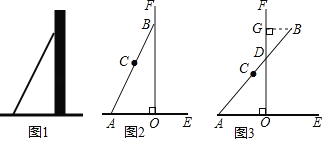
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
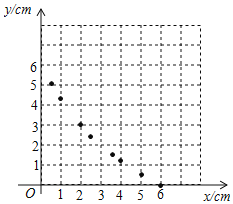
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.