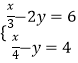题目内容
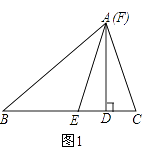
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(-1,0),C(0,-5)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q. 若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
【答案】(1)y=x-3;y=x2-2x-3;(2)P1(-2,5),P2(1,-4)(3)存在, ![]()
【解析】试题分析:(1)、根据抛物线的对称轴和点A的坐标得出点B的坐标,然后将点B和点C的坐标代入解析式得出一次函数解析式,将二次函数设成交点式,然后将点C的坐标代入求出二次函数的解析式;(2)、根据题意得出AB=4,OB=OC=3,则∠OCB=∠OBC=45°,设抛物线的对称轴与x轴交于点M,MB=2,然后分B为直角顶点和C为直角顶点两种情况分别求出点P的坐标;
(3)、首先设出点Q的坐标,然后得出点Q到直线BC的距离,然后根据点Q到直线BC的距离等于半径得出答案.
点晴:本题主要考查的就是函数解析式的求法、直角三角形的性质、切线的性质以及分类讨论思想.求函数解析式我们一般采用待定系数法进行求解.
在函数里面出现几何问题时,一定要注意分类讨论,然后根据直角三角形直角顶点的不同位置,从而得出两种不同的情况,分别根据直角三角形的性质得出答案.
在解决这种类型的题目时我们一定要注意分类讨论以及根据特殊三角形的性质进行解答,即使有一种不符合题意的情况也需要进行说明,最后根据实际情况进行舍去即可.
在直线和圆的位置关系中,当圆心到直线的距离等于半径时,则直线与圆相切,对于这种问题分别利用公式得出圆与直线的距离和圆的半径,然后根据相等列出方程得出答案.
试题解析:(1)∵对称轴为x=2,且抛物线经过A(1,0), ∴B(3,0).
把B(3,0)、C(0,3)分别代入y=mx+n,
得![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=x-3;
∵对称轴为x=1,且抛物线经过A(-1,0),
∴点B(3,0),
设y=a(x-3)(x+1),
把C(0,-3)代入解得:a=1,
故解析式为:y=x2-2x-3;
(2)由(1)得:AB=4,OB=OC=3,
∴∠OCB=∠OBC=45°.
设抛物线的对称轴与x轴交于点M,则MB=2.
①如图,若B为直角顶点,
设BP交抛物线的对称轴为点N1,则∠MBP=45°,
∴N1M=MB=2,即N1(1,2),
则直线N1B的表达式为y=-x+3, ![]() ,
,
解得![]() (舍去),
(舍去), ![]() ,所以P1(-2,5);
,所以P1(-2,5);

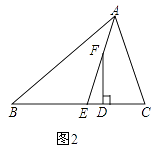
②如图,若C为直角顶点,设BP交抛物线的对称轴为点N2,过点N2作y轴的垂线,垂足为点E,
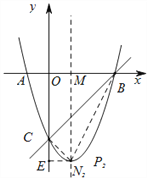
则∠PCE=45°,∴CE=EN2=OM=1,∴ON2=4,即N2(1, -4),
则直线N2C的表达式为y=-x-3, ![]() ,
,
解得![]() (舍去),
(舍去), ![]() ,
,
所以P2(1,-4);综上所述,满足条件的点P共有两个,分别为P1(-2,5),P2(1,-4);
(3)存在,最大⊙Q的半径为![]() .
.

【题目】计算机中常用的十六进制是逢16进1的记数制,采用数字0~9和字母A~F共16个记数符号,这些符号与十进制的数对应关系如下表:
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | …… |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | …… |
例如,用十六进制表示:5+A=F,E+2=10,D+F=1C,则在16进制下,B+E=____.(用十六进制数填)