题目内容

若反比例函数y=
k
x
（k＜0）的图象上有两点P1（2，y1）和P2（3，y2），那么（　　）
A、y1＜y2＜0
B、y1＞y2＞0
C、y2＜y1＜0
D、y2＞y1＞0
练习册系列答案
相关题目
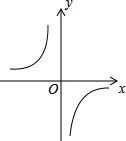已知函数y=
m
x
的图象如图，以下结论：
①m＜0；
②在每个分支上y随x的增大而增大；
③若点A（-1，a）、点B（2，b）在图象上，则a＜b；
④若点P（x，y）在图象上，则点P1（-x，-y）也在图象上．
其中正确的个数是（　　）
A、4个B、3个C、2个D、1个
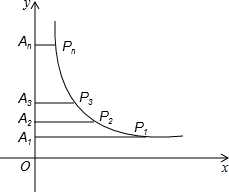如图，在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An（n为正整数），过点A1，A2，A3，…，An分别作y轴的垂线，与反比例函数y=
2
x
（x＞0）交于P1，P2，P3，…，Pn，连接P1P2，P2P3，P3P4，…，Pn-1Pn，得梯形A1A2P2P1，A2A3P3P2，A3A4P4P3，…，AnAn+1Pn+1Pn，设其面积分别为S1，S2，S3，…，Sn，则Sn=（　　）
A、
2n
n(n-1)
B、
2n-1
n(n-1)
C、
2n
n(n+1)
D、
2n+1
n(n+1)
如图，反比例函数y=
a
x
（a＞0）与y=-
a
x
的图象上的四个点A、B、C、D构成正方形，它的各边与坐标平行．若正方形的对角线长为4
2
，则a的值为（　　）
A、4B、8C、12D、16
若点A（1，y1）、B（2，y2）都在反比例函数y=
2
x
的图象上，则y1、y2的大小关系为（　　）
A、y1≤y2
B、y1≥y2
C、y1＜y2
D、y1＞y2
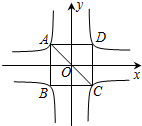
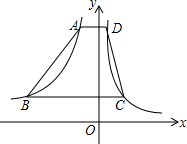如图，在横跨第一、二象限的梯形ABCD中，AD∥BC∥x轴，AD=1，BC=4，它的高为4，四个顶点都在反比例函数的图象上，则关于A、B两点坐标说法正确的是（　　）
A、A点的横坐标是-
3
5
，B点的横坐标是-3
B、A点的横坐标是-
3
5
，B点的纵坐标是
4
3
C、A点的纵坐标是
16
3
，B点的横坐标是-3
D、A点的纵坐标是
16
3
，B点的纵坐标是
4
3
已知点P（m，-1）在反比例函数y=-
3
x
的图象上，则m的值为（　　）
A、-3B、-1C、3D、1
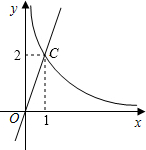反比例函数y=
k
x
和正比例函数y=mx的部分图象如图，由此可以得到方程
k
x
=mx的实数根为（　　）
A、x=1
B、x=2
C、x1=1，x2=-1
D、x1=1，x2=-2
在△ABC中，若AB=AC=15，BC=24，若P是△ABC所在的平面内的点，且PB=PC=20，则AP的长为（　　）
A、7B、5C、7或25D、5或14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网