题目内容

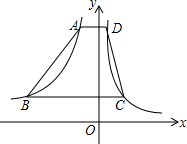如图，在横跨第一、二象限的梯形ABCD中，AD∥BC∥x轴，AD=1，BC=4，它的高为4，四个顶点都在反比例函数的图象上，则关于A、B两点坐标说法正确的是（　　）
A、A点的横坐标是-
3
5
，B点的横坐标是-3
B、A点的横坐标是-
3
5
，B点的纵坐标是
4
3
C、A点的纵坐标是
16
3
，B点的横坐标是-3
D、A点的纵坐标是
16
3
，B点的纵坐标是
4
3
练习册系列答案
相关题目
反比例函数y=
k-1
x
的图象位于第二、四象限，则k的取值范围是（　　）
A、k≥1B、k＞1
C、k＜1D、k≤1
如图，两个反比例函数y=
6
x
和y=
3
x
在第一象限内的图象依次是C1和C2，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，则四边形PAOB的面积为（　　）
A、2B、3C、3.5D、4
已知点P1（x1，y1），P2（x2，y2）均在双曲线y=
2m+3
x
上，当x1＜x2＜0时，y1＜y2，那么m的取值范围是（　　）
A、m＞
3
2
B、m＞-
3
2
C、m＜
3
2
D、m＜-
3
2
若反比例函数y=
k
x
（k＜0）的图象上有两点P1（2，y1）和P2（3，y2），那么（　　）
A、y1＜y2＜0
B、y1＞y2＞0
C、y2＜y1＜0
D、y2＞y1＞0
若点A（-2，y1）、B（-1，y2）、C（1，y3）在反比例函数y=-
1
x
的图象上，则（　　）
A、y1＞y2＞y3
B、y3＞y2＞y1
C、y1＞y3＞y2
D、y2＞y1＞y3
如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=
k
x
（k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，
2
3
），过点E的直线l交x轴于点F，交y轴于点G（0，-2），则点F的坐标是（　　）
A、（
5
4
，0）
B、（
7
4
，0）
C、（
9
4
，0）
D、（
11
4
，0）
若正比例函数y=3x与反比例函数y=
k
x
（k≠0）的图象相交，则当x＞0时，交点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
如图，A、B、C为3×3正方形网格的三个个点，则tan∠ABC等于（　　）
A、
1
2
B、
1
3
C、
2
3
D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网