题目内容

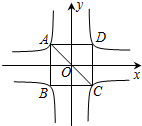如图，反比例函数y=
a
x
（a＞0）与y=-
a
x
的图象上的四个点A、B、C、D构成正方形，它的各边与坐标平行．若正方形的对角线长为4
2
，则a的值为（　　）
A、4B、8C、12D、16
练习册系列答案
相关题目
函数y=kx+2与y=
k
x
在同一坐标系内的图象可以是（　　）
A、
B、
C、
D、
如图，反比例函数y=-
6
x
在第二象限的图象上有两点A、B，它们的横坐标分别为-1，-3，直线AB与x轴交于点C，则△AOC的面积为（　　）
A、8B、10C、12D、24
如图，两个反比例函数y=
6
x
和y=
3
x
在第一象限内的图象依次是C1和C2，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，则四边形PAOB的面积为（　　）
A、2B、3C、3.5D、4
已知反比例函数y=
k
x
的图象经过点（2，3），那么下列四个点中，也在这个函数图象上的是（　　）
A、（-6，1）
B、（1，6）
C、（2，-3）
D、（3，-2）
已知点P1（x1，y1），P2（x2，y2）均在双曲线y=
2m+3
x
上，当x1＜x2＜0时，y1＜y2，那么m的取值范围是（　　）
A、m＞
3
2
B、m＞-
3
2
C、m＜
3
2
D、m＜-
3
2
若反比例函数y=
k
x
（k＜0）的图象上有两点P1（2，y1）和P2（3，y2），那么（　　）
A、y1＜y2＜0
B、y1＞y2＞0
C、y2＜y1＜0
D、y2＞y1＞0
如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=
k
x
（k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，
2
3
），过点E的直线l交x轴于点F，交y轴于点G（0，-2），则点F的坐标是（　　）
A、（
5
4
，0）
B、（
7
4
，0）
C、（
9
4
，0）
D、（
11
4
，0）
如图，△ABC中，BC=AC，D、E两点分别在BC与AC上，AD⊥BC，BE⊥AC，AD与BE相交于F点．若AD=4，CD=3，则关于∠FBD、∠FCD、∠FCE的大小关系，下列何者正确？（　　）
A、∠FBD＞∠FCDB、∠FBD＜∠FCDC、∠FCE＞∠FCDD、∠FCE＜∠FCD

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网