��Ŀ����
����Ŀ����1���������֤����������
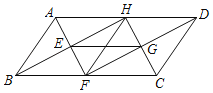
��֪����ͼ��ֱ��AB��CD��ֱ��EF���أ�AB��CD��EGƽ�֡�BEF��FGƽ�֡�DFE��EG��FG���ڵ�G����֤��EG��FG��

֤������AB��CD����֪��
���BEF+��DFE=180�㣨______����
��EGƽ�֡�BEF��FGƽ�֡�DFE����֪����
��______��______��______����
���GEF+��GFE=![]() ����BEF+��DFE����______����
����BEF+��DFE����______����
���GEF+��GFE=![]() ��180��=90�㣨______����
��180��=90�㣨______����
�ڡ�EGF�У���GEF+��GFE+��G=180�㣨______����
���G=180��-90��=90�㣨��ʽ���ʣ���
��EG��FG��______����
��2��������������д����1����֤���⣺______��
���𰸡���1������������2������ƽ���߱�������ֱ�����أ�ͬ���ڽǵ�ƽ�����ഹֱ
��������
��1���ȸ���AB��CD�����BEF���DFE�Ĺ�ϵ�����ɽ�ƽ���ߵ����������FEG+��EFG�Ķ�����Ȼ�����������ڽǺͶ������������EGF�Ķ����������ɵý��ۣ�
��2�����ݣ�1���Ľ���д����֤���⼴�ɣ�
��1��֤������AB��CD����֪����
���BEF+��DFE=180������ֱ��ƽ�У�ͬ���ڽǻ�������
��EGƽ�֡�BEF��FGƽ�֡�DFE����֪����
���GEF=![]() ��BEF����GFE=
��BEF����GFE=![]() ��DFE����ƽ���ߵĶ��壩��
��DFE����ƽ���ߵĶ��壩��
���GEF+��GFE=![]() ����BEF+��DFE������ʽ�����ʣ���
����BEF+��DFE������ʽ�����ʣ���
���GEF+��GFE=![]() ��180��=90����������������
��180��=90����������������
�ڡ�EGF�У���GEF+��GFE+��G=180���������ε��ڽǺͶ�������
���G=180����90��=90������ʽ���ʣ���
��EG��FG�� ��ֱ�Ķ��壩��
��2�����������Կɱ�ʾΪ������ƽ���߱�������ֱ�����أ�ͬ���ڽǵ�ƽ�����ഹֱ��
�ʴ�Ϊ������ƽ���߱�������ֱ�����أ�ͬ���ڽǵ�ƽ�����ഹֱ��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�