ЬтФПФкШн
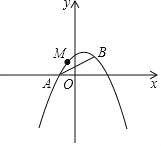
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНax2+bx+1ОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ1ЃЌ1ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдФЖСРэНтЃК
дкЭЌвЛЦНУцжБНЧзјБъЯЕжаЃЌжБЯпl1ЃКyЃНk1x+b1ЃЈk1ЃЌb1ЮЊГЃЪ§ЃЌЧвk1Ёй0ЃЉЃЌжБЯпl2ЃКyЃНk2x+b2ЃЈk2ЃЌb2ЮЊГЃЪ§ЃЌЧвk2Ёй0ЃЉЃЌШєl1ЁЭl2ЃЌдђk1k2ЃНЉ1ЃЎ
НтОіЮЪЬтЃК
ЂйШєжБЯпyЃН2xЉ1гыжБЯпyЃНmx+2ЛЅЯрДЙжБЃЌдђmЕФжЕЪЧ____ЃЛ
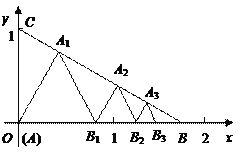
ЂкХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁїPABЪЧвдABЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉMЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЧвдкжБЯпABЕФЩЯЗНЃЈВЛгыAЃЌBжиКЯЃЉЃЌЧѓЕуMЕНжБЯпABЕФОрРыЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2+
x2+![]() x+1ЃЛЃЈ2ЃЉЂй-
x+1ЃЛЃЈ2ЃЉЂй-![]() ЃЛЂкЕуPЕФзјБъЃЈ6ЃЌЉ14ЃЉЃЈ4ЃЌЉ5ЃЉЃЛЃЈ3ЃЉ
ЃЛЂкЕуPЕФзјБъЃЈ6ЃЌЉ14ЃЉЃЈ4ЃЌЉ5ЃЉЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИљОнДЙЯпМфЕФЙиЯЕЃЌПЩЕУPAЃЌPBЕФНтЮіЪНЃЌИљОнНтЗНГЬзщЃЌПЩЕУPЕузјБъЃЛ
ЃЈ3ЃЉИљОнДЙжБгкxЕФжБЯпЩЯСНЕуМфЕФОрРыЪЧНЯДѓЕФзнзјБъМѕНЯаЁЕФзнзјБъЃЌПЩЕУMQЃЌИљОнШ§НЧаЮЕФУцЛ§ЃЌПЩЕУЖўДЮКЏЪ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЃЌПЩЕУУцЛ§ЕФзюДѓжЕЃЌИљОнШ§НЧаЮЕФЕзвЛЖЈЪБУцЛ§гыИпГЩе§БШЃЌПЩЕУШ§НЧаЮИпЕФзюДѓжЕ
НтЃКЃЈ1ЃЉНЋAЃЌBЕузјБъДњШыЃЌЕУ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ХзЮяЯпЕФНтЮіЪНЮЊyЃНЉ![]() x2+
x2+![]() x+1ЃЛ
x+1ЃЛ
ЃЈ2ЃЉЂйгЩжБЯпyЃН2xЉ1гыжБЯпyЃНmx+2ЛЅЯрДЙжБЃЌЕУ
2mЃНЉ1ЃЌ
МДmЃНЉ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃКЉ![]() ЃЛ
ЃЛ
ЂкABЕФНтЮіЪНЮЊyЃН![]() x+
x+![]() ЃЌ
ЃЌ
ЕБPAЁЭABЪБЃЌPAЕФНтЮіЪНЮЊyЃНЉ2xЉ2ЃЌ
СЊСЂPAгыХзЮяЯпЃЌЕУ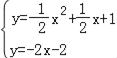 ЃЌ
ЃЌ
НтЕУ![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ![]() ЃЌ
ЃЌ
МДPЃЈ6ЃЌЉ14ЃЉЃЛ
ЕБPBЁЭABЪБЃЌPBЕФНтЮіЪНЮЊyЃНЉ2x+3ЃЌ
СЊСЂPBгыХзЮяЯпЃЌЕУ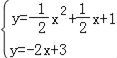 ЃЌ
ЃЌ
НтЕУ![]() ЃЈЩсЃЉ
ЃЈЩсЃЉ![]() ЃЌ
ЃЌ
МДPЃЈ4ЃЌЉ5ЃЉЃЌ
злЩЯЫљЪіЃКЁїPABЪЧвдABЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃЌЕуPЕФзјБъЃЈ6ЃЌЉ14ЃЉЃЈ4ЃЌЉ5ЃЉЃЛ
ЃЈ3ЃЉШчЭМЃК
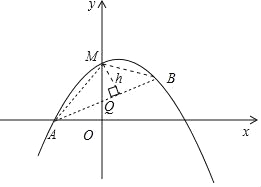 ЃЌ
ЃЌ
ЁпMЃЈtЃЌЉ![]() t2+
t2+![]() t+1ЃЉЃЌQЃЈtЃЌ
t+1ЃЉЃЌQЃЈtЃЌ![]() t+
t+![]() ЃЉЃЌ
ЃЉЃЌ
ЁрMQЃНЉ![]() t2+
t2+![]()
SЁїMABЃН![]() MQ|xBЉxA|
MQ|xBЉxA|
ЃН![]() ЃЈЉ
ЃЈЉ![]() t2+
t2+![]() ЃЉЁС2
ЃЉЁС2
ЃНЉ![]() t2+
t2+![]() ЃЌ
ЃЌ
ЕБtЃН0ЪБЃЌSШЁзюДѓжЕ![]() ЃЌМДMЃЈ0ЃЌ1ЃЉЃЎ
ЃЌМДMЃЈ0ЃЌ1ЃЉЃЎ
гЩЙДЙЩЖЈРэЃЌЕУ
ABЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЩшMЕНABЕФОрРыЮЊhЃЌгЩШ§НЧаЮЕФУцЛ§ЃЌЕУ
hЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЕуMЕНжБЯпABЕФОрРыЕФзюДѓжЕЪЧ![]() ЃЎ
ЃЎ

 ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИЁОЬтФПЁПАЫФъМЖЮяРэаЫШЄаЁзщ20ЮЛЭЌбЇдкЪЕбщВйзїжаЕФЕУЗжШчБэЃК
ЕУЗжЃЈЗжЃЉ | 10 | 9 | 8 | 7 |
ШЫЪ§ЃЈШЫЃЉ | 5 | 8 | 4 | 3 |
ЃЈ1ЃЉЧѓет20ЮЛЭЌбЇЪЕбщВйзїЕУЗжЕФжкЪ§ЃЌжаЮЛЪ§ЃЛ
ЃЈ2ЃЉет20ЮЛЭЌбЇЪЕбщВйзїЕУЗжЕФЦНОљЗжЪЧЖрЩйЃП