题目内容
【题目】对于三个数a,b,c,用max{a,b,c}表示这三个数中最大数,例如:max{-2,1,0}=1,max![]()
解决问题:
(1)填空:max{1,2,3}=______,如果max{3,4,2x-6}=2x-6,则x的取值范围为______;
(2)如果max{2,x+2,-3x-7}=5,求x的值;
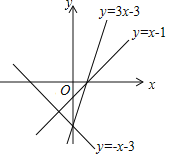
(3)如图,在同一坐标系中画出了三个一次函数的图象:y=-x-3,y=x-1和y=3x-3请观察这三个函数的图象,
①在图中画出max{-x-3,x-1,3x-3}对应的图象(加粗);
②max{-x-3,x-1,3x-3}的最小值为______.
【答案】(1)3;x≥5;(2)x的值为4或3;(3)①见解析;②-2.
【解析】
(1)根据max{a,b,c}表示这三个数中最大数,进行解答即可;
(2)分情况讨论:①当x+2=5时,②当3x7=5时,分别解方程,然后进行验证即可;
(3)①三个一次函数图象中,上方的部分就是max{-x-3,x-1,3x-3}对应的图象;
②由图象可以知,max{x3,x1,3x3}的最小值为直线y=x3与y=x1的交点纵坐标,联立解析式求出交点坐标即可.
解:(1)1,2,3中3为最大数,故max{1,2,3}=3,
∵max{3,4,2x6}=2x6,
∴2x6≥4,
解得x≥5,
故答案为:3;x≥5;
(2)∵max{2,x+2,3x7}=5,
∴①当x+2=5时,解得x=3,验证得3×37=16<5,成立,
②当3x7=5时,解得x=4,验证得4+2=2<2<5,成立
故max{2,x+2,3x7}=5时,x的值为4或3;
(3)①如图所示:
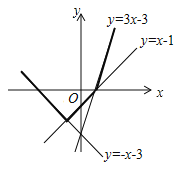
②由图象可以知,max{x3,x1,3x3}的最小值为直线y=x3与y=x1的交点纵坐标,
联立![]() ,解得:
,解得:![]() ,
,
∴max{-x-3,x-1,3x-3}的最小值为2.