题目内容
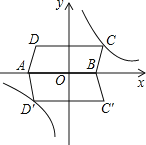
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(﹣4,0),B(2,0),C(3,3)反比例函数![]() 的图象经过点C.
的图象经过点C.
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B,请你通过计算说明点D′在双曲线上;
(3)请你画出△AD′C,并求出它的面积.
【答案】解:(1)∵点C(3,3)在反比例函数![]() 的图象上,∴
的图象上,∴![]() 。∴m=9。
。∴m=9。
∴反比例函数的解析式为![]() 。
。
(2)过C作CE⊥x轴于点E,过D作DF⊥x轴于点F,则△CBE≌△DAF,
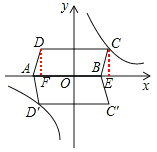
∴AF=BE,DF=CE。
∵A(﹣4,0),B(2,0),C(3,3),
∴DF=CE=3,OA=4,OE=3,OB=2。
∴![]() 。
。
∴D(﹣3,3)。
∵点D′与点D关于x轴对称,∴D′(﹣3,﹣3)。
把x=﹣3代入![]() 得,y=﹣3,∴点D′在双曲线上。
得,y=﹣3,∴点D′在双曲线上。
(3)作图如下:
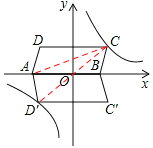
∵C(3,3),D′(﹣3,﹣3),∴点C和点D′关于原点O中心对称。
∴D′O=CO=![]() D′C。
D′C。
∴S△AD′C=2S△AOC=2×![]() AOCE=2×
AOCE=2×![]() ×4×3=12。
×4×3=12。
【解析】
试题(1)把点C(3,3)代入反比例函数![]() ,求出m,即可求出解析式。
,求出m,即可求出解析式。
(2)过C作CE⊥x轴于点E,过D作DF⊥x轴于点F,则△CBE≌△DAF,根据线段之间的数量关系进一步求出点D的坐标,再点D′与点D关于x轴对称,求出D′坐标,进而判断点D′是不是在双曲线。
(3)根据C(3,3),D′(﹣3,﹣3)得到点C和点D′关于原点O中心对称,进一步得出D′O=CO=![]() D′C,由S△AD′C=2S△AOC=2×
D′C,由S△AD′C=2S△AOC=2×![]() AOCE求出面积的值。
AOCE求出面积的值。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目