题目内容
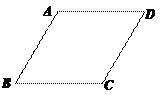
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.

(1)求证:△ADG≌△CDG.
(2)若![]() =
=![]() ,EG=4,求AG的长.
,EG=4,求AG的长.
【答案】(1)证明见解析;(2)AG=6 .
【解析】分析:(1)首先根据菱形的性质得到∠ADG=∠CDG,AD=BC,然后根据“SAS”推出△ADG≌△CDG;
(2)先证明△FAE∽△FBC,可得![]() ,再证明△DGE∽△BGC,求出CG的长,从而可求出AG的长.
,再证明△DGE∽△BGC,求出CG的长,从而可求出AG的长.
详解:(1)∵四边形ABCD是菱形,
∴AB=BC,AD=BC,
又∵BD=BD,
∴△ABD≌△CBD,
∴∠ADB=∠CDB,
又∵AD=CD,DG=DG,
∴△ADG≌△CDG.
(2)∵△ADG≌△CDG,
∴AG=GC,
∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∴△FAE∽△FBC,
∴![]() =
=![]() ,
,
∵![]() =,
=,
∴![]() =,
=,
∴![]() =,
=,
∴![]() =.
=.
∵AD∥BC,
∴∠GDE=∠GBC,∠GED=∠GCB,又∠DGE=∠BGC,
∴△DGE∽△BGC,
∴![]() =
=![]() =,
=,
∵EG=4,
∴CG=6,
∴AG=6 .

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目