题目内容
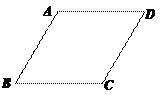
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为多少?( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]() -1
-1
【答案】D
【解析】分析:分三种情形讨论①若以边BC为底.②若以边PC为底.③若以边PB为底.分别求出PD的最小值,即可判断.
详解::在菱形ABCD中,
∵∠ABC=60°,AB=1,
∴△ABC, △ACD都是等边三角形,
①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“,即当点P与点A重合时,PD值最小,最小值为1;
②若以边PB为底, ∠PCB为顶角,以点C为圆心,BC为半径作圆,则弧BD上的点A与点D均满足△PBC为等腰三角形,当点P与点D重合时,PD最小,显然不满足题意,故此种情况不存在;
③若以边PC为底, ∠PBC为顶角时,以点B为圆心,BC长为半径作圆,与BD相交于一点,则弧AC(除点C外)上的所有点都满足△PBC是等腰三角形,当点P在BD上时,PD最小.

∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC=CD=AD,∠ABC=∠ADC=60°,
∴△ABC,△ADC是等边三角形,
∴BO=DO=sin60 ×1=![]() ,
,
∴BD=2BO=2×![]() =
=![]() ,
,
∴PD =BD-BP=![]() -1.
-1.
∵![]() -1<1,
-1<1,
∴PD的最小值为![]() -1.
-1.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
初中部 | a | 85 | b | s初中2 |
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差s初中2,并判断哪一个代表队选手成绩较为稳定.










