题目内容
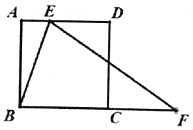
【题目】在□ABCD中,∠BAD,∠BCD的平分线分别交BC,AD于点F,E.
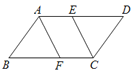
(1)求证:四边形AFCE是平行四边形;
(2)若BF=4,FC=3,求□ABCD的周长.
【答案】(1)见解析;(2)22.
【解析】分析:(1)根据角平分线的定义以及平行线的性质,证明∠1=∠2,再由平行线的性质,得到∠3=∠4,即可得到结论;
(2)先求出AB的长,再利用平行四边形的周长公式进行解答即可.
详解:(1)∵ABCD是平行四边形,∴AD∥BC,∠BAD=∠BCD.
∵AF、CE分别平分∠BAD、∠BCD,
∴∠1=![]() ∠BAD,∠2=
∠BAD,∠2=![]() ∠BCD,
∠BCD,
∴∠1=∠2.
∵AD∥BC,
∴∠1+∠3=1800 ∠2+∠4=180°,
∴∠3=∠4.
又∵∠1=∠2,
∴AFCE是平行四边形.
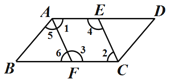
(2)∵AF平分∠BAD,∴∠1=∠5.
∵AD∥BC,∴∠1=∠6,∴∠5=∠6,∴AB=BF=4,
∴□ABCD的周长=2(AB+BC)=2(4+4+3)=22.

练习册系列答案
相关题目
【题目】如表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同.
课外小组活动总时间/h | 文艺小组活动次数 | 科技小组活动次数 | |
七年级 | 12.5 | 4 | 3 |
八年级 | 10.5 | 3 | 3 |
九年级 | 7 | ☆ | ☆ |
则九年级文艺小组活动次数和科技小组活动次数(表中的两个五星)分别是( )
A.2,2B.1,3C.3,1D.1,2