ЬтФПФкШн
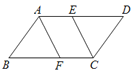
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌвдЯпЖЮOAЮЊБпдкЕкЫФЯѓЯоФкзїЕШБпШ§НЧаЮЁїAOBЃЌЕуCЮЊxе§АыжсЩЯвЛЖЏЕуЃЈOCЃО2ЃЉЃЌСЌНгBCЃЌвдЯпЖЮBCЮЊБпдкЕкЫФЯѓЯоФкзїЕШБпШ§НЧаЮЁїCBDСЌНгDAВЂбгГЄНЛyжсгкЕуEЃЎ

ЃЈ1ЃЉдкЕуCЕФдЫЖЏЙ§ГЬжаЃЌЁїOBCКЭЁїABDШЋЕШТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉдкЕуCЕФдЫЖЏЙ§ГЬжаЃЌЁЯCADЕФЖШЪ§ЪЧЗёЛсБфЛЏЃПШчЙћВЛБфЃЌЧыЧѓГіЁЯCADЕФЖШЪ§ЃЛШчЙћБфЛЏЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЬНОПЕБЕуCдЫЖЏЕНЪВУДЮЛжУЪБЃЌвдAЃЌEЃЌCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃП
ЁОД№АИЁПЃЈ1ЃЉЁїOBCКЭЁїABDШЋЕШЃЌРэгЩМћНтЮіЃЌЃЈ2ЃЉВЛЛсЗЂЩњБфЛЏЃЌ60ЁуЃЌЃЈ3ЃЉЕБЕуCЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЪБЃЌвдAЃЌEЃЌCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнЕШБпШ§НЧаЮЕФаджЪЕУЁЯOBAЃНЁЯCBDЃН60ЁуЃЌOBЃНBAЃЌBCЃНBDЃЌдђЁЯOBCЃНЁЯABDЃЌШЛКѓПЩИљОнЁАSASЁБПЩХаЖЈЁїOBCЁеЁїABDЃЛ
ЃЈ2ЃЉгЩЁїAOBЪЧЕШБпШ§НЧаЮжЊЁЯBOAЃНЁЯOABЃН60ЁуЃЌдйгЩЁїOBCЁеЁїABDжЊЁЯBADЃНЁЯBOCЃН60ЁуЃЌИљОнЁЯCADЃН180ЁуЉЁЯOABЉЁЯBADПЩЕУНсТлЃЛ
ЃЈ3ЃЉЯШИљОнШЋЕШШ§НЧаЮЕФаджЪвдМАЕШБпШ§НЧаЮЕФаджЪЃЌЧѓЕУЁЯEACЃН120ЁуЃЌНјЖјЕУГівдAЃЌEЃЌCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЪБЃЌAEКЭACЪЧбќЃЌзюКѓИљОнRtЁїAOEжаЃЌOAЃН2ЃЌЁЯOEAЃН30ЁуЃЌЧѓЕУACЃНAEЃН4ЃЌОнДЫЕУЕНOCЃН6ЃЌМДПЩЕУГіЕуCЕФЮЛжУЃЎ
ЃЈ1ЃЉЁїOBCКЭЁїABDШЋЕШЃЌРэгЩЪЧЃК
ЁпЁїAOBЃЌЁїCBDЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрOBЃНABЃЌCBЃНDBЃЌЁЯABOЃНЁЯDBCЃЌ
ЁрЁЯOBCЃНЁЯABDЃЌ
дкЁїOBCКЭЁїABDжаЃЌ
Ёп ЃЌ
ЃЌ
ЁрЁїOBCЁеЁїABDЃЈSASЃЉЃЛ
ЃЈ2ЃЉЕуCдкдЫЖЏЙ§ГЬжаЃЌЁЯCADЕФЖШЪ§ВЛЛсЗЂЩњБфЛЏЃЌРэгЩШчЯТЃК
ЁпЁїAOBЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBOAЃНЁЯOABЃН60ЁуЃЌ
ЁпЁїOBCЁеЁїABDЃЌ
ЁрЁЯBADЃНЁЯBOCЃН60ЁуЃЌ
ЁрЁЯCADЃН180ЁуЉЁЯOABЉЁЯBADЃН60ЁуЃЛ
ЃЈ3ЃЉЁпЁїOBCЁеЁїABDЃЌ
ЁрЁЯBOCЃНЁЯBADЃН60ЁуЃЌ
гжЁпЁЯOABЃН60ЁуЃЌ
ЁрЁЯOAEЃН180ЁуЉ60ЁуЉ60ЁуЃН60ЁуЃЌ
ЁрЁЯEACЃН120ЁуЃЌЁЯOEAЃН30ЁуЃЌ
ЁрвдAЃЌEЃЌCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЪБЃЌAEКЭACЪЧбќЃЌ
ЁпЕуAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌ
ЁрOAЃН2ЃЌ
дкRtЁїAOEжаЃЌЁЯOEAЃН30ЁуЃЌ
ЁрAEЃН4ЃЌ
ЁрACЃНAEЃН4ЃЌ
ЁрOCЃН2+4ЃН6ЃЌ
ЁрЕБЕуCЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЪБЃЌвдAЃЌEЃЌCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЎ

 ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИ
ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИ