��Ŀ����
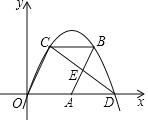
����Ŀ����ͼ�٣�������y=a(x2+2x-3)(a��0)��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����OC=OB.
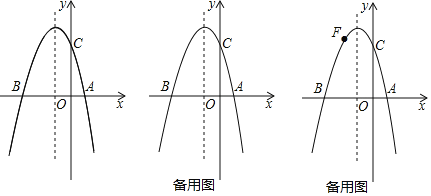
(1)ֱ��д����B��������( �� )�����������ߵĽ���ʽ��
(2)���D�������ߵĶ��㣬�����ߵĶԳ�����ֱ��l������BD���߶�OC�ϵĵ�E����ֱ��l�ĶԳƵ�E'ǡ�����߶�BD�ϣ����E�����ꣻ
(3)����FΪ�����ߵڶ�����ͼ���ϵ�һ�����㣬����BF��CF������BCF������ǡ�ABC�����һ��ʱ�����ʱ��F������.
���𰸡�(1)-3��0��y=-x2-2x+3��(2)��0��2����(3)��-2��3����-1��4��
��������
��1���ⷽ��a��x2+2x-3��=0�ɵ�B��-3��0����A��1��0������C��0��-3a����������OB=OC�õ�-3a=3�����a=-1���Ӷ��õ������߽���ʽ��
��2����ͼ�ڣ���һ��ʽ�䷽�õ�y=-��x+1��2+4����D��-1��4�������ô���ϵ�������ֱ��BD�Ľ���ʽΪy=2x+6����E��0��t�������öԳƵ����ʵ�E����-2��t����Ȼ���E����-2��t������y=2x+6���t���Ӷ��õ���E�����ꣻ
��3����ֱ��BC�Ľ���ʽΪy=x+3����FG��y�ύֱ��BC��G����ͼ�ۣ���F��x��-x2-2x+3����-3��x��0������G��x��x+3��������FG=-x2-3x�����������������ʽ�õ�S��FBC=![]() ��3����-x2-3x����Ȼ��������BCF���������ABC�����һ��õ�
��3����-x2-3x����Ȼ��������BCF���������ABC�����һ��õ�![]() ��3����-x2-3x��=
��3����-x2-3x��=![]() ��
��![]() ��4��3��Ȼ��ⷽ�����x�Ӷ��õ�F������꣮
��4��3��Ȼ��ⷽ�����x�Ӷ��õ�F������꣮
��1����y=0ʱ��a��x2+2x-3��=0�����x1=-3��x2=1����B��-3��0����A��1��0����
��x=0ʱ��y=-3a����C��0��-3a����
��OB=OC��
��-3a=3�����a=-1��
�������߽���ʽΪy=-x2-2x+3��
�ʴ�Ϊ-3��0��
��2����ͼ��
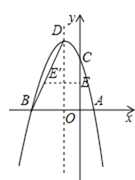
��y=-x2-2x+3=-��x+1��2+4��
��D��-1��4����
��ֱ��BD�Ľ���ʽΪy=kx+b��
��B��-3��0������-1��4�������![]() �����
�����![]() ��
��
��ֱ��BD�Ľ���ʽΪy=2x+6��
��E��0��t����
��E�������E����ֱ��x=-1�Գƣ�
��E����-2��t����
��E����-2��t������y=2x+6��t=-4+6=2��
���E��������0��2����
��3����ֱ��BC�Ľ���ʽΪy=x+3����FG��y�ύֱ��BC��G����ͼ��
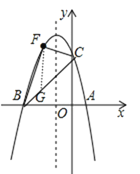
��F��x��-x2-2x+3����-3��x��0������G��x��x+3����
��FG=-x2-2x+3-��x+3��=-x2-3x��
��S��FBC=![]() ��3����-x2-3x����
��3����-x2-3x����
�ߡ�BCF���������ABC�����һ�룬
��![]() ��3����-x2-3x��=
��3����-x2-3x��=![]() ��
��![]() ��4��3�����x1=-1��x2=-2��
��4��3�����x1=-1��x2=-2��
��F���������-2��3����-1��4����

����Ŀ��������![]() �ϲ��ֵ�ĺ�����
�ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ���±���
�Ķ�Ӧֵ���±���
| �� |
|
|
|
|
| �� |
| �� |
|
|
|
|
| �� |
![]() �����ϱ���գ�
�����ϱ���գ�
����������![]() ��Ľ���������________��________��
��Ľ���������________��________��
�������߾�����![]() ,________
,________![]() ��
��
���ڶԳ����Ҳ࣬![]() ��
��![]() �����________��
�����________��
![]() ��ȷ��������
��ȷ��������![]() �Ľ���ʽ��
�Ľ���ʽ��