题目内容
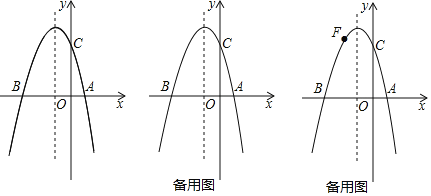
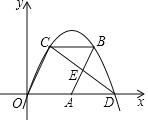
【题目】如图,点A为x轴上一点,点B的坐标为(a,b),以OA,AB为边构造OABC,过点O,C,B的抛物线与x轴交于点D,连结CD,交边AB于点E,若AE=BE,则点C的横坐标为( )
A.a﹣bB.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
利用平行四边形的性质得BC∥OA,BC=OA,设C(t,b),则BC=a﹣t,再证明△EBC≌△EAD得到BC=AD=a﹣t,从而得到抛物线的对称轴为直线x=a﹣t,所以a﹣t﹣t=a﹣(a﹣t),然后解关于t的方程即可.
解:∵四边形OABC为平行四边形,
∴BC∥OA,BC=OA,
设C(t,b),则BC=a﹣t,
∵BC∥AD,
∴∠EBC=∠EAD,
在△EBC和△EAD中
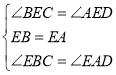 ,
,
∴△EBC≌△EAD(ASA),
∴BC=AD=a﹣t,
∴点A为OD的中点,
∴抛物线的对称轴为直线x=a﹣t,
∴a﹣t﹣t=a﹣(a﹣t),
∴t=![]() a.
a.
故选:C.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
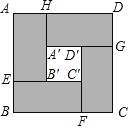
【题目】创客联盟的队员想用3D打印完成一幅边长为4米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形A′B′C′D′,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如下表
材料 | 甲 | 乙 |
价格(元/米2) | 60 | 30 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
(1)A′D′的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于3时,预备材料的购买资金700元够用吗?请利用函数的增减性来说明理由.