题目内容
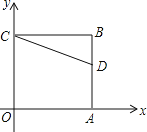
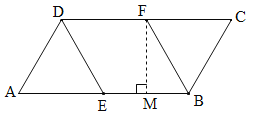
【题目】如图,在□ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4.
(1)求证:△AED≌△CFB;
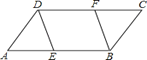
(2)当四边形DEBF为菱形时,求出该菱形的面积;
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题(1)首先根据平行四边形的性质可得AD=BC,∠A=∠C,再加上条件AE=CF可利用SAS证明△AED≌△CFB;
(2)作FM⊥AB于M,可以得到△BFC是等边三角形,得到∠FBM=60°,再求出菱形的高FM,从而得到菱形的面积.
解答:证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,
在△ADE和△CBF中,∵AD=BC,∠A=∠C,AE=CF,∴△AED≌△CFB(SAS);
(2)作FM⊥AB于M,
在菱形DEBF中,BE=BF=![]() AB=
AB=![]() ,∵CF=
,∵CF=![]() CD=
CD=![]() ,BC=AD=
,BC=AD=![]() AB=2,∴CF=BC=BF,∴△BFC是等边三角形,∴∠BFC=60°,∵ABCD是平行四边形,∴AB∥CD,∴∠MBF=∠BFC=60°,∴∠FBM=30°,∴MB=
AB=2,∴CF=BC=BF,∴△BFC是等边三角形,∴∠BFC=60°,∵ABCD是平行四边形,∴AB∥CD,∴∠MBF=∠BFC=60°,∴∠FBM=30°,∴MB=![]() BF=1,∴FM=
BF=1,∴FM=![]() MB=
MB=![]() ,∴菱形DEBF的面积=BEFM=
,∴菱形DEBF的面积=BEFM=![]() .
.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目