题目内容
如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.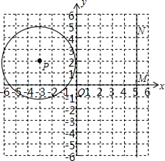
(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长.

解:(1)如图所示,⊙P′即为所求作的圆。
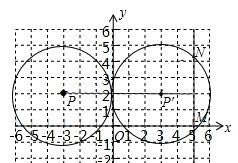
⊙P′与直线MN相交。
(2)设直线PP′与MN相交于点A,
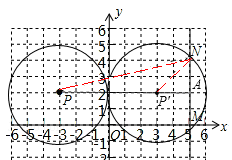
则由⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在⊙P′上,得
P′N=3,AP′=2,PA=8。
∴在Rt△AP′N中,
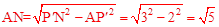 。
。
在Rt△APN中,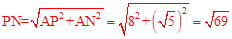 。
。
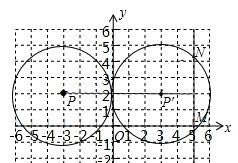
⊙P′与直线MN相交。
(2)设直线PP′与MN相交于点A,

则由⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在⊙P′上,得
P′N=3,AP′=2,PA=8。
∴在Rt△AP′N中,
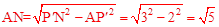 。
。在Rt△APN中,
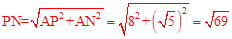 。
。网格问题,作图(轴对称变换),直线与圆的位置关系,勾股定理。
(1)根据关于y轴对称的点的横坐标互为相反数,纵坐标相等找出点P′的位置,然后以3为半径画圆即可。再根据直线与圆的位置关系解答。
(2)设直线PP′与MN相交于点A,在Rt△AP′N中,利用勾股定理求出AN的长度,在Rt△APN中,利用勾股定理列式计算即可求出PN的长度。
(1)根据关于y轴对称的点的横坐标互为相反数,纵坐标相等找出点P′的位置,然后以3为半径画圆即可。再根据直线与圆的位置关系解答。
(2)设直线PP′与MN相交于点A,在Rt△AP′N中,利用勾股定理求出AN的长度,在Rt△APN中,利用勾股定理列式计算即可求出PN的长度。

练习册系列答案
相关题目
 .
. ;
;
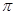
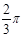
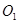 的半径
的半径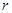 为3cm,⊙
为3cm,⊙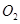 的半径
的半径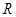 为4cm,两圆的圆心距
为4cm,两圆的圆心距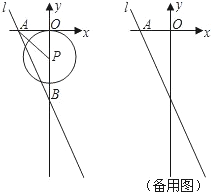
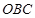 ,
,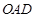 的半径之间的关系是
的半径之间的关系是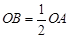 ,则弧BC的长是弧AD长的( )
,则弧BC的长是弧AD长的( )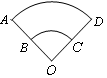
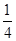 倍
倍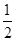 倍
倍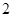 倍
倍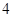 倍
倍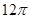 ,圆心角为
,圆心角为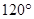 ,则该扇形的半径为 .
,则该扇形的半径为 .